حساب مساحة منطقة بالتكامل 
المساحة تحت بين منحنى ومحور السينات :
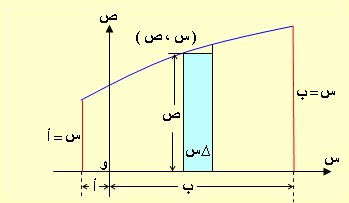
سيكون كلامنا على دالة معرفة ومحدودة في [ أ ، ب ] وبالنظر للشكل
ولحساب مساحة المنطقة المحددة بالمنحنى ومحور السينات والمستقيمين
الموازيين لمحور الصادات ( س = أ ، س = ب) نأخذ النقطة ( س ، ص )
على المنحنى ولنأخذ جزءاً صغيراً من مساحة المنطقة بطول ص وبعرض
∆ س وبفرض ∆ م مساحة هذا الجزء أي ∆ م = ص × ∆ س وتكون:

ب
وبصورة أخرى بالتعويض عن ص بدلالة س يكون : المساحة المطلوبة = ∫ د(س) دس
أ
يجب ملاحظة الإشارة هنا فالمساحة ص . ∆ س وباعتبار ∆ س موجبة فتكون ص محددة للإشارة وهي موجبة فوق محور السينات وسالبة أسفله
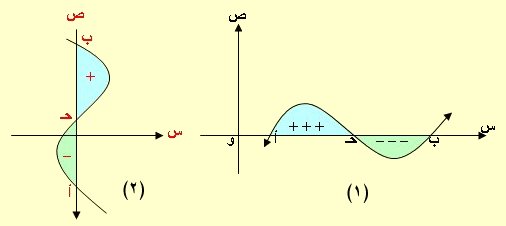
فإن كان جزء من المنحنى أعلى محور السينات وآخر تحته فالتكامل يكون الفرق بين المساحتين كما مبين بالشكل(1) ،
ب
المساحة المطلوبة = ∫ ص د س = الفرق بين المساحتين " الزرقاء – الخضراء"
أ
وفي حالة حساب المساحة بين المنحنى ومحور الصادات وباعتبار ∆ ص موجبة فإن س هي التي تحدد الإشارة فالجزء الواقع على يمين محور
الصادات(المنحنى) يكون موجب وما يقع على يساره سالب كما في الشكل(2)
ب
المساحة المطلوبة = ∫ س د ص = الفرق بين المساحتين " الزرقاء – الخضراء" ولكن لحساب المساحة بين المنحنى ومحور الصادات
أ
يكون ناتج جمع المساحتين حسابياً بصرف النظر عن الإشارة
ب
وعلى العموم تكون المساحة = | ∫ ص د س | ونرمز م(ق) عادة للمساحة هنا أو م أو أي رمز آخر للدلالة عليها.
أ
وحساب المساحة أما أن يكون :
(1) مباشر بإعطاء معادلة المنحنى والفترة
(2) غير مباشر بإعطاء المنحنى وحساب نقط التقاطع مع المحور ويكون التكامل من الأولى للثاني + من الثانية للثالثة + ...
(3) المساحة بين منحيين بحل معادلتهم لمعرفة نقط التقاطع
(4) مساحة منطقة محدودة بمنحنى مغلق
(5) المساحة بطريقة الأشباه المنحرفة أنظـر هنـا
(6) المساحة بطريقة سمبسون أنظـر هنـا
لقد بينا قانون حساب المساحة لكل من (1) ، (2) المبين في أعلاه وسنورد الآن القانون الخاص بالحالة رقم (3) للمساحة بين منحنيين
ليكن ص = د1(س) ، ص = د2(س) هما المنحنيين المبينان في الشكل 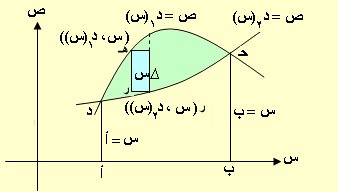
حيث حـ ، د نقط تقاطعهم ، س = أ ، س = ب الاحداثيان السينيان لهما
ولنأخذ شريحة مستطيلة الشكل طوله هـ ر وعرضه ∆ س حيث الاحداثي
الصادي للنقطة هـ هو د1(س) وللنقطة ر هو د2(س) فتكون :
مساحة المستطيل = هـ ر × ∆ س
= [ د1(س) – د2(س)] × ∆ س

ب
المساحة المطلوبة = ∫ [ د1(س) – د2(س)] د س
أ
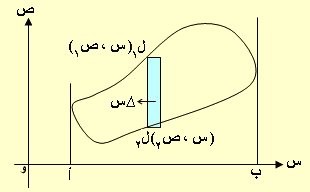
أما بالنسبة لرقم (4) مساحة المنطقة المحدودة بمنحنى مغلق
الشكل يمثل منحنى الدالة ص = د(س) ولإيجاد مساحة المنطقة المغلقة ، نأخذ أحداثي رأسي بين المماسين للمنحنى المبينين بالشكل على يمين ويسار المنحنى والموازيين لمحور الصادات قاطعاً المنحنى في ل1 ، ل2 حيث ل1( س ، ص1) ، ل2( س ، ص2) فيكون ل1 ل2 = ص1 – ص2 ولنأخذ شريحة صغيرة مستطيلة الشكل طولها ل1 ل2 وعرضها ∆ س فتكون مساحتها = ( ص1 – ص2 ) . ∆ س " المبينة باللون الأزرق فتكون :
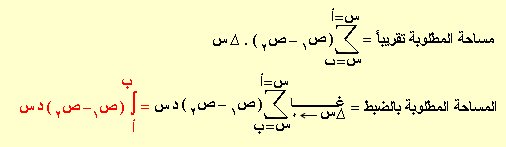
تنبيه : أ ، ب هما قيمتا س اللتان تكون عندها ص1= ص2 أي أن ص1 – ص2 = 0 والمساحة المطلوبة لا علاقة لها بقطع المنحنى المحورين