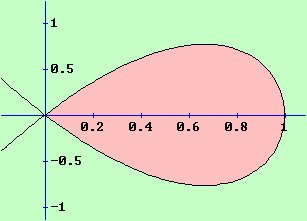
مثال(4) : أحسب المساحة التي يحيط بها منحنى الدالة  ص² = 4 س² – 4 س³

الحـــل :

ص² = 4 س² – 4 س³

ص² = 4 س²(1 – س )

                       ـــــــــــــ

 ص = ± 2 س /\1– س

                      ـــــــــــــ

 ص₁ = 2 س /\1– س

                        ـــــــــــــ

 ص₂ = –2 س /\1– س

                                ـــــــــــــ

ص₁ –  ص₂ = 4 س /\1– س  = صفر

س = صفر  أو  س = 1 حدا التكامل

                                            ب

  نعلم أن : المساحة المطلوبة = | ∫ ( ص₁ –  ص₂ ) د س |  فتكون :

                                            أ

                                 1           ـــــــــــــ

  المساحة المطلوبة  = | ∫  4 س /\1– س  د س |

                                0         

بوضع  ع² = 1 – س فيكون 2 ع د ع = – د س أي د س = – 2ع دع ، وتكون س = 1 – ع² ، س = 0 فإن ع = 1 ، س = 1 فإن  س = 0

                                 0

  المساحة المطلوبة  = | ∫  4(1 – ع²) × ع × – 2 ع د ع |           ذلك من التعويض د س = – 2ع دع  ، واستبدال س بـ ع

                               1

                                 0

  المساحة المطلوبة  = | ∫  ( –8ع²+ 8ع⁴ ) د ع |          بفك القوس وإجراء عملية التكامل

                               1

                                 0

                                       8ع³    8ع⁵

  المساحة المطلوبة  = | ∫  – ــــــ +  ـــــــ  |                  بالتعويض عن حدا التكامل نجد أن :

                               1      3        5

                                                  8       8              بإجراء العمليات الحسابية

  المساحة المطلوبة  = |  صفر – ( – ــــــ + ـــــــ )|  

                                                  3       5

                               16

 المساحة المطلوبة  =  ـــــ

                              15