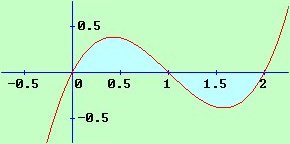
أحسب المساحة المحصورة بين منحنى الدالة ص = س3–3 س2 +2 س ومحور السينات
الحـــل :
محور السينات معادلته ص = 0 ، نضع ص = 0 لمعرفة نقط تقاطع المنحنى المعطى مع محور السينات
س3–3 س2 +2 س = 0 بأخذ س عامل مشترك
س( س2– 3 س + 2 ) = 0 بتحليل المقدار الثلاثي
س( س – 1)( س – 1) = 0 بوضع كل منها بالصفر
س = 0 أو س = 1 أو س = 2 نقط التقاطع (0، 0) ، (1، 0) ، (2، 0) لاحظ الرسم واتصال الدالة في [0، 2]
ب
نعلم أن : المساحة المطلوبة = | ∫ ص د س | حيث ص = س3–3 س2 +2 س ، أ = 0 ، حـ = 1 ، ب = 2 فيكون
أ
1 2
المساحة المطلوبة = | ∫ ص د س
| + | ∫ ص د س
| 
0 1
1 2
م(ق) = | ∫ (س3–3 س2 +2 س) د س | + | ∫ (س3–3 س2 +2 س) د س |
0 1
1
2
س4 3س3 2س2 س4 3س3 4س2
م(ق) = | [( ــــــ – ــــــ + ـــــــ ) ] | + | [( ــــــ – ــــــ + ـــــــ ) ] |
4 3 2 0 4 3 2 1
س4 1 س4 2
م(ق) = | [( ــــــ – س3+ س2 ) ] | + | [( ــــــ – س3+ س2 ) ] |
4 0 4 1
1 16 1
م(ق) = | ( ــــ – 1+ 1 ) – صفر | + | ( ــــــ – 8 + 4) – ( ــــ – 1 + 1 ) |
4 4 4
1 1 1 1 1
م(ق) = | ــــ | + | (0) – ( ــــ ) | = ـــــ + ــــــ = ـــ وحدة مساحة
4 4 4 4 2