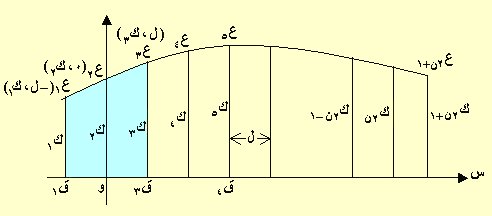
طريقة سمبسون تعين المساحة بدقة أكثر من طريقة الأشباه المنحرفة وتتم بأخذ ثلاث نقط متتالية ع1(– ل، ك1)، ع2( 0، ك2)، ع3( ل، ك3 ) على المنحنى باعتبار المنحنى المار بها من الدرجة الثانية ( أ س2 + ب س + حـ ) ومنه ننطلق لحساب المساحة التقريبية المطلوبة، فالشكل التالي :

قسمنا هنا البعد بين العامودين عند طرفي المنحنى لعدد زوجي(2 ن) من الفترات الجزئية المتساوية طول كل منها ل ونرسم الأعمدة كما مبين بالشكل تقابل المنحنى في النقط ع1، ع2، ع3 ، ... ، ع2ن+1 ولنأخذ المنحنى المار بالنقط الثلاثة ع1، ع2، ع3 وهو من الدرجة الثانية وتكون المساحة هنا تحت المنحى وفوق المحور و س ، والمستقيمين ع1 ق1 ، ع3 ق3 هي
ل ل
∫ ص د س = ∫ ( أ س2 + ب س + حـ ) د س
– ل – ل
ل
1 1
= [ ــــ أ س3 + ــــ ب س2 + حـ س ]
3 2
– ل
بالتعويض هنا وعن النقاط الثلاثة في معادلة المنحنى وحل المعادلات الناتجة للتخلص من أ ، ب ، حـ نحصل على
1
المساحة بالتقريب = ـــ ل[( ك1 + ك2ن+1) + 2(ك3+ ك5+ ك7+ ...+ك2ن–1) + 4(ك2+ ك4+ ك6+ ...+ك2ن )]
3