ما سبق من حساب المساحة المحدودة
بمنحنى أشترط فيها وجود معادلة المنحنى وكذلك وجود ناتج للتكامل وهما شرطان ليس
بالضرورة وجودهم دوماً في حياتنا العملية وبالتالي يكون حساب المساحة لمنحنيات لا
يتوفر فيها الشرطان السابقان يتم بطرق تقريبية وهي كثيرة معتمدين على أن التكامل
يعبر عنه هندسياً بمساحة محدودة لمنحنى الدالة ومن طرق حساب المساحة هذه استخدام
الأشباه المنحرفة.

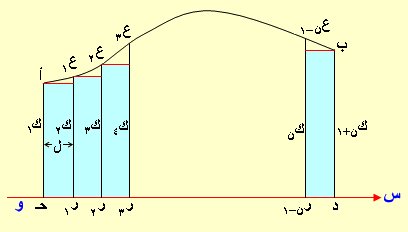
الشكل الآتي يبين مساحة محدودة بالمنحنى أ ب ، والمستقيم و س والمستقيمين حـ أ ، د ب حيث قسمنا البعد حـ د لأجزاء متساوية في الطول ل مثلاً بالنقط ر1، ر2، ر3، .... ، رن–1 وبإقامة أعمدة من هذه النقط ك1 ، ك2 ، ك3 ، ك4 ، كن ، كن+1 تلاقي المنحنى في النقط ع1، ع2، ع3، ... ، عن–1 ونصل بين كل نقطتين متتاليتين فنحصل على مجموعة من أشباه المنحرف والمعروف بمساحته التي تساوي نصف مجموع قاعدتيه مضروباً في الارتفاع ويكون مجموع مساحتها مساوياً تقريباً للمساحة المحدودة بالمنحى والمستقيم و س والمستقيمين أ حـ ، ب د.
ويمكن حساب المساحة تقريباً بمجموع مساحات أشباه المنحرف أي
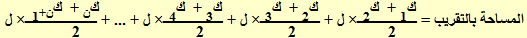
1
المساحة بالتقريب = ل [ ـــــ ( ك1 + كن+1 ) + ك2+ ك3+ ك4 + .... + كن ]
2
وكلما ازداد عدد الأجزاء كلما كانت النتيجة أكثر دقة
5
ــــــــــــــــــ
مثال : احسب بطريقة الأشباه المنحرفة ∫ /\1 + س3 د س
1
الحـل :
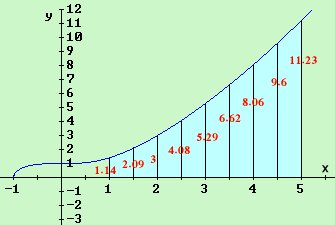
برسم المنحنى بين س = 1 ، س = 5 وذلك بتكوين الجدول الآتي:
| س | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 |
| ص | 1.14 | 2.09 | 3 | 4.08 | 5.29 | 6.62 | 8.06 | 9.6 | 11.23 |
1
المساحة بالتقريب = ل [ ـــــ ( ك1 + كن+1 ) + ك2+ ك3+ ك4 + .... + كن ]
2
1
المساحة بالتقريب = 0.5[ ـــــ (1.14 + 11.23 ) + 2.09+ 3+ 4.08+ 5.29+ 6.62 + 8.06 + 9.6]
2
المساحة بالتقريب = 0.5( 6.19 + 2.09+ 3 + 4.08+ 5.29+ 6.62 + 8.06 + 9.6]
المساحة بالتقريب = 0.5( 44.93)
المساحة بالتقريب = 22.47