زوايا الارتفاع والانخفاض

الهدف إيجاد ارتفاع أو بعد بين جسمين باستخدام نقط للرصد بينهم وهي من المسائل العملية لزوايا الارتفاع والانخفاض وهي عدة أنواع تعتمد في حساباتها على دقة الرسم ومعرفة القوانين.

النوع الأول: إيجاد طول تل أو ما شابه ذلك.  النوع الثاني  النوع الثالث   مثال1  مثال2  مثال3   مثال4  مثال5

مثال:

شاهد رجل من نقطة في المستوى الأفقي المار بسفح تل أن زاوية ارتفاع قمة التل 15^¯10^ه وبعد أن صعد مسافة 1000متر على مستوى يميل على الأفقي بزاوية 30^¯7^ه وجدَ أن قياس زاوية ارتفاع قمة التل هي 40^¯15^ه . أحسب ارتفاع التل.   

 الحـل:

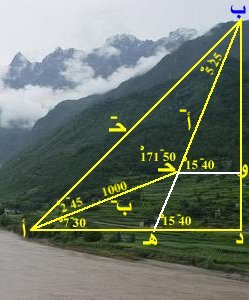
الشكل المقابل يوصف الحالة التي نحن بصددها، ب د ارتفاع التل (ع) ، أ نقطة الرصد الأولى ( زاوية د أ ب ) عند سفح التل حيث تحرك على أ حـ فقاس زاوية ارتفاع قمة التل من حـ (زاوية ب حـ و) وعليه نعمل حساباتنا كالتالي:

 < د أ ب = 15^¯10^ه ، < د أ حـ = 30^¯7^ه زاوية ميل المستوى،

< و حـ ب = 40^¯15^ه = < د هـ ب لأن حـ و // هـ د

<د هـ ب = < أ ب هـ + < هـ أ ب  الزاوية الخارجة عن المثلث أ ب هـ

40^¯15^ه = < أ ب هـ + 15^¯10^ه  ومنها

< أ ب هـ = 40^¯15^ه – 15^¯10^ه = 25^¯5^ه

< ب أ حـ = 15^¯10^ه – 30^¯7^ه = 45^¯2^ه 

أصبح المثلث أ ب حـ معلوم منه زاويتان ب، حـ وضلع أ حـ = 1000متر

فيمكن إيجاد الزاوية الثالثة وهي أ حـ ب

< أ حـ ب = 180^ه– ( 45^¯2^ه + 25^¯5^ه ) = 180^ه –  10^¯8^ه  =  50^¯171^ه 

   ب^¯      حـ¯  

ـــــــــ = ــــــــــ    من المثلث أ ب حـ وقاعدة الجيب

حاب      حاحـ

             ب¯ حاحـ     1000حا50^¯171^ه  

  حـ^¯ = ــــــــــــــــــ = ــــــــــــــــــــــــــــــــــــ    .............. (1)

              حاب                حا25^¯5^ه

ومن المثلث ب د أ يكون د ب = حـ^¯ × حا أ = حـ^¯ × حا 15^¯10^ه  ، د ب هو ارتفاع البرج

           1000حا50^¯171^ه  

 د ب = ــــــــــــــــــــــــــــــــــــ × حا 15^¯10^ه      وباستخدام الآلة الحاسبة أو أي طريقة أخرى نجد أن:

                حا25^¯5^ه

د ب = 267.775 متر تقريباً