زوايا الارتفاع والانخفاض
الهدف إيجاد ارتفاع أو بعد بين جسمين باستخدام نقط للرصد بينهم وهي من المسائل العملية لزوايا الارتفاع والانخفاض وهي عدة أنواع تعتمد في حساباتها على دقة الرسم ومعرفة القوانين.
النوع الثاني: إيجاد ارتفاع جسم لا يمكن الوصول لقاعدته
حيث يكون الموقع المطلوب ونقطتا الرصد في مستوى أفقي واحد في حين البعد بين نقطتي الرصد والارتفاع لا يقعا في مستوى واحد بمعنى أن الموقع و نقطتا الرصد ليست على استقامة واحدة، وتوجد طرق ثلاث لهذا النوع نبينها كالتالي:
1) من الشكل:

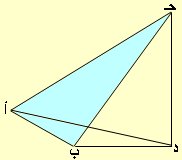
نقيس أ ب (أ ، ب نقطتا الرصد) ، د قاعدة الجسم المراد قياس ارتفاعه نقيس زاوية ارتفاع حـ من أ حيث حـ قمة الجسم المراد معرفة ارتفاعه وهي < د أ حـ ، ونعرف < ب أ حـ بين الاتجاهين أب ، أ حـ وكذلك < أ ب حـ يمكن الآن حساب طول أ حـ من المثلث أ ب حـ وحيث أن المثلث أ حـ د قائم وعلم <أ ، أ حـ فيمكن معرفة طول حـ د الارتفاع المطلوب
2) كما سبق نعين أ ، ب والبعد بينهم ونقيس زاوية ارتفاع حـ من أ وهي < د أ حـ حيث حـ قمة الجسم المراد معرفة ارتفاعه وهنا نقيس < ب أ د بين الاتجاهين أ ب ، ب د ، ومن ب نقيس الزاوية أ ب د بين الاتجاهين ب أ ، ب د والحل كما سبق بمعرفة طول أ د ، ومن المثلث القائم أ حـ د نحسب الارتفاع حـ د.
3) نعين أ ، ب بحيث يكون أ ب عمودي على أ د ونقيس أ ب ونقيس زاويتا الارتفاع < د أ حـ ، < د ب حـ والحل يكون من المثلث أ حـ د القائم نعبر عن أ د بدلالة حـ د ومن المثلث القائم أ ب د يمكن حساب حـ د.
مثال:
إذا كانت زاوية ارتفاع منطاد
من محطة رصد على سطح الأرض تقع في جنوبه فكانت 35¯45ه
وفي نفس الوقت كانت زاوية ارتفاعه من محطة ثانية شرق المحطة الأولى وعلى بعد 725
متر منها فكانت 22¯40ه
أوجد ارتفاع المنطاد.
الحــل:
من المثلث القائم أ د حـ:
أ د = د حـ طتا(د أ حـ) = ع طتا35¯45ه
من المثلث القائم ب د حـ:
ب د = د حـ طتا(د ب حـ) = ع طتا22¯40ه
(أ ب)2 = (ب د)2– (أ د)2 لاحظ الشكل ق<(ب أ د)=90ه
(725)2 = ع2 طتا2(22¯40ه ) – ع2 طتا2(35¯45ه)
= ع2[طتا2(22¯40ه ) – طتا2(35¯ 45ه)]
(725)2
ع2 = ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
طتا2(22¯ 40ه ) – طتا2(35¯ 45ه)
ومنها ع = 1114 متراً تقريباً عند لحظة الرصد للمنطاد.