زوايا الارتفاع والانخفاض

زوايا الارتفاع والانخفاض

الهدف إيجاد ارتفاع أو بعد بين جسمين باستخدام نقط للرصد بينهم وهي من المسائل العملية لزوايا الارتفاع والانخفاض وهي عدة أنواع تعتمد في حساباتها على دقة الرسم ومعرفة القوانين.

النوع الثالث: إيجاد البعد بين مرئيين لا يمكن الوصول إليهما:

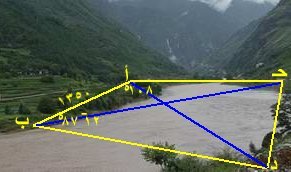
مثل مكانيين على ضفتي نهر والرصد من الضفة الأخرى وتكون هنا النقاط الأربع للمكانيين ومكانا الرصد في مستوى أفقي واحد ويتم الرصد هنا للزوايا من الضفة الأخرى بعد تحديد مكانيين عليها ومعرفة البعد بينهم وقياس الزوايا كما هو مبين بالمثال الآتي:

حـ ، د قلعتان على ضفة نهر رصدتا من مكانيين أ ، ب البعد بينهم 1350متر فوجد < حـ أ ب = 108^ه ، < د أ ب = 12^¯43^ه ، < حـ ب أ = 10^¯32^ه ، < د ب أ = 12^¯87^ه . احسب البعد بين القلعتين.

الحل:

في المثلث أ ب حـ ، < أ= 108^ه ، < ب = 10^¯32^ه ، حـ^¯= 1350 متر فتكون < حـ = 180^ه – ( 108^ه + 10^¯32^ه ) = 50^¯39^ه

ومن قاعدة الجيب نجد أن:

1350 حا 10^¯32^ه

ب¯ = ـــــــــــــــــــــــــــــــــــــ وباستخدام الآلة الحاسبة يكون

حا 50^¯39^ه

ب¯ = 1119متر أي أن أ حـ = 1119 متر

في المثلث أ ب د:

< أ= 12^¯43^ه ، < ب = 12^¯87^ه ، حـ^¯= 1350متر فتكون < د = 180^ه – ( 12^¯43^ه + 12^¯87^ه ) = 36^¯49^ه

ومن قاعدة الجيب نجد أن:

1350 حا 12^¯87^ه

ب¯ = ـــــــــــــــــــــــــــــــــــــ وباستخدام الآلة الحاسبة يكون

حا 36^¯49^ه

ب¯ = 1770متر أي أن أ د = 1770 متر

في المثلث أ حـ د ، د^¯= 1119 متر ، حـ^¯= 1770 متر

< حـ أ د = 108^ه – 12^¯43^ه = 48^¯64^ه

ومن قاعدة ظل نصف الفرق نجد أن:

حـ – د حـ¯ – د¯ أ

طا ــــــــــــــ = ـــــــــــــــــــــــــ طتا ــــ

2 حـ¯+ د¯ 2

حـ – د 1770– 1119

طا ــــــــــــــ = ــــــــــــــــــــــــــــــ طتا 24¯32^ه وباستخدام الآلة الحاسبة يكون

2 1770 + 1119

حـ – د

ــــــــــــــ = 33^¯19^ه ولكن

حـ + د

ــــــــــــــ = 36^¯57^ه وبالجمع تكون < حـ = 9^¯77^ه

1770 حا 48^¯64^ه

أ¯ = ـــــــــــــــــــــــــــــــــــــ ، أ¯ هو حـ د ، وباستخدام الآلة الحاسبة يكون

حا 9^¯77^ه

أ¯ = 1644 متر وهو البعد المطلوب