الانحدار الخطي البسيط ( Regression)        طريقة المربعات الصغرى        الانحدار المتعدد        الانحدار غير الخطي        تقدير تباين خط الانحدار

مقدمــة:

    تهدف دراسة الانحدار التنبوء بقيمة متغير (Y)  بمعرفة متغير آخر (X) ويعرف المتغير الأول بالمتغير التابع (dependent) ويرمز له Y ويقاس دون خطأ في حين يعرف المتغير الآخر بالمتغير المستقل (Independent) ويرمز له X فإذا أعطينا قيمة ما (أي قيمة تنتمي لمجموعة الأعداد الحقيقية) للمتغير X في المعادلة Y = α + β X فنحصل علي قيمة مناظرة للمتغير Y فهنا قيمة Y تتحدد بمعرفة قيمة X فلذا المتغير X عرف بالمتغير المستقيل في حين Y تتعين قيمتها تبعاً لقيمة X لذا عرفت Y بالمتغير التابع (أي تبعاً لقيمة X)، كما أن الانحدار هنا بسيط لوجود متغيرين فقط تابع ومستقل، وسنتحدث لاحقاً عن الانحدار المتعدد بوجود متغير تابع واحد فقط مع وجود وجود متغيرين مستقلين أو أكثر، وعند ذكر كلمة الخط نعني بها خط الانحدار.

    والانحدار يعني بالبحث عن هذه المعادلة أو العلاقة بين المتغيرين X المستقل ، Y التابع أو المعتمد كما أن المعادلة Y = α + β X تحوي α , β وهما قيمتان ثابتتان حيث β تبين ميل الخط المستقيم Y = α + β X (الزاوية التي يصنعها المستقيم مع الاتجاه الموجب لمحور السينات) وإن إشارة α تعني:

• أن تكون β موجبة فإن علاقة Y  بالمتغير المستقل X علاقة طردية موجبة ( تزداد قيم Y بزيادة قيم X المناظرة لها أو العكس أي تنقص بنقصانها).

• أن تكون β موجبة فإن الخط Y = α + β X يصنع زاوية حادة مع محور السينات الموجب كما مبين بالشكل.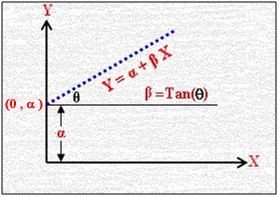

• أن تكونβ =  صفراً فتنعدم العلاقة الخطيبة (لا توجد علاقة) وأن قيمة Y ثابتة (  y = α ).

• أن تكون β = ∞ فتنعدم العلاقة الخطيبة (لا توجد علاقة) كما في الشكل.

• تعرف β بميل الانحدار

• أن تكون β سالبة فإن العلاقة عكسية سالبة (تزداد قيم Y بنقص قيم X المناظرة لها أو العكس).

• في حين أن α تبين قيمة الجزء المقطوع من محور الصادات (الرأسي) بالمستقيم Y = α + β X

• الخط Y = α + β X يمر بالنقطة ( 0 ، α ) أو أن الخط Y = α + β X يمر بالزوج ( 0, α )

• تعرف α بثابت الانحدار

• عند استخدام عينه n من الأزواج من مجتمع ذو بعدين فنكتب العلاقة بحروف صغيرة Y = a + b X ويكون:

• a تقديراً لـ α و b تقديراً لـ  β.

وتسمى المعادلة Y = a + b X بمعادلة انحدار Y على X  في حين X = a + b Y معادلة X على Y سواء للعينة أو المجتمع ولمعرفة المعادلة يجب معرفة كل من a , b ويجدر هنا القول إن اهتمامنا يكون على العلاقة نفسها ببين X , Y وليس على سبب وجود العلاقة أو الظروف المحيطة بها فهناك علاقة سببية بين كمية السماد وكمية الناتج الزراعي للقمح مثلاً ولكننا لا يمكن أن نجزم بوجود علاقة سببية لعدد المساكن وميزانية الدولة.

تقرأ معادلة خط الانحدار بأن Y دالة في X .