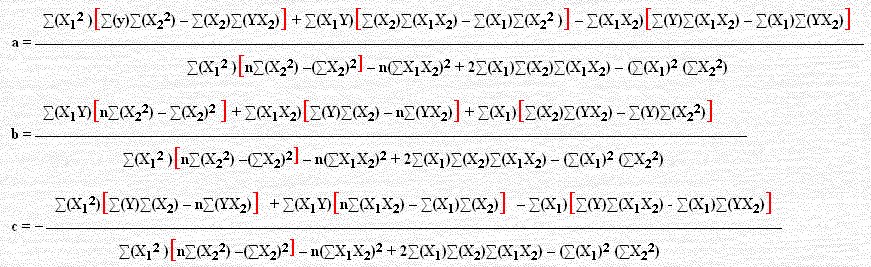
الانحدار المتعدد
سبق أن تكلمنا عن الانحدار البسيط ممثلاً في معادلة خط انحداره Y = α + βX والتي تظهر المتغير التابع Y المعتمد على المتغير المستقل X وسندرس الآن المتغير التابع مرتبطاً بأكثر من متغير مستقل وهو ما يمكن معالجته بالانحدار البسيط بتأثير كل المتغيرات المستقلة معاً على المتغير التابع وهو ما يقودنا لانحدار المتعدد (أكثر من متغير مستقل X1, X2, ..., Xn) بقصد التنبؤ بالمتغير التابع والذي يأخذ معادلة انحداره ( X2X1/ Y ) الصورة الآتية:
μY/X1X2 = α + β1X1+ + β2X2 + β3X3+ ... + βkXk + ε
أو اختصاراً
μY = α + β1X1+ + β2X2 + β3X3+ ... + βkXk + ε
وإذا أخذنا المعادلة:
μY = α + β1X1+ β2X2 حيث X1, X2 متغيران مستقلان ، Y المتغير التابع ، α , β1 , β2 ثوابت وأن β1 معامل انحدار X1/ Y وأن β2 معامل انحدار X2 / Y .
وتحت نفس الشروط الأربع السابق ذكرها في الانحدار البسيط ( توزيع معتدل ، متوسط صفر , تباين ثابت ، استقلالية الأخطاء) مع إضافة تساوي التباينات لقيم X1, X2
وسوف نمثل المعادلة
μY
= α + β1X1+ β2X2
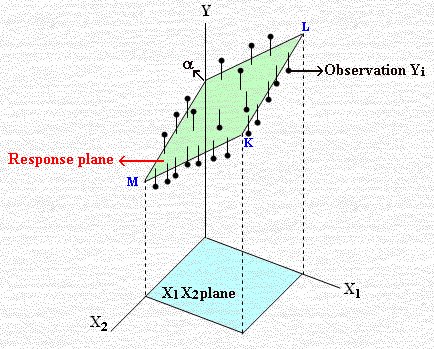
في الفراغ ذو
الثلاثة أبعاد كما مبين بالشكل المقابل, وهذه
صورة -
Picture
مجرد توضيح للانحدار الهرمي.
من الواضح إن المستوى العمودي على المحور X1 جميع نقاطه لها نفس القيمة X1 وهو (هنا X1 ثابت) ما يعني تثبيت أثر المتغير X1 وتقاطع هذا المستوى مع مستوى الانحدار (الأخضر) سيكون خط مستقيم (المستويان يتقاطعان في خط مستقيم ) ميله β2 ميل خط انحدار X1/ Y، لماذا؟ قلنا إن X1 ثابت فإن β1X1 ثابت ، α ثابت فالمعادلة أعلاه μY = α + β1X1+ β2X2 تأخذ الصورة μY = X2 + β2X2 حيث X2 قيمة ثابتة تساوي α + β1X1 وواضح من المعادلة السابقة (μY = X2 + β2X2 ) الميل يساوي β2 ، بالمثل تثبيت X2 يعطينا مستوى يقطع مستوى الانحدار في خط مستقيم ميلهβ1 (خط انحدار X1 / Y ). لاحظ النقطة ( X1 , X2 , Y ) في حالة X1 = X2 = 0 فإن Y = α من التعويض في المعادلة μY = α + β1X1+ β2X2 أي المستوى الأخضر يقطع Y في النقطة التي إحداثها الصادي = α كما مبين بالشكل.
من الواضح إننا نبحث انحدار متغير
(عامل) واحد (التابع) على آخر (مستقل) مع تثبيت أثر العوامل الأخرى (المتغيرات
الأخرى بتثبيتها) وهنا سنستخدم تقديرات العينة
 كتقدير لعينات المجتمع فتصبح المعادلة بالصورة:
Y = a + bX1+ cX2 (لمتغيرين
مستقلين مع المتغير التابع
أو أي رموز أخرى بدلاً عن a, b, c .
كتقدير لعينات المجتمع فتصبح المعادلة بالصورة:
Y = a + bX1+ cX2 (لمتغيرين
مستقلين مع المتغير التابع
أو أي رموز أخرى بدلاً عن a, b, c .
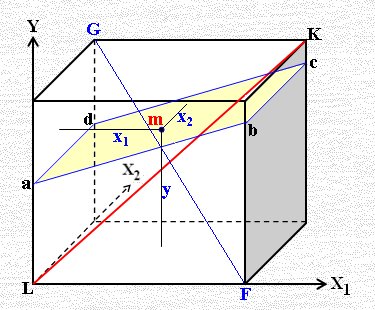
أي أن: a, b, c تقديرات لـ α , β1 , β2 والتي تجعل مجموع مربعات أبعاد النقط المشاهدة (Observation المبينة في الشكل) للمسافات الرأسية 2( Y – Yi)∑ أقل ما يمكن أي: [Y – (α + β1X1 + β2X2 + β3X3+ ... + βkXk)]2
وبالتفاضل الجزئي لكل من a, b, c على التوالي نحصل على المعادلات الثلاثة التالية ومن ثم جعل كل ناتج يساوي صفر ( شروط وجود النهاية الصغرى).
∑Y = na + b∑X1 + c ∑X2
∑X1Y = a∑X1 + b∑X12 + c ∑X1X2
∑X2Y = a∑X2 + b∑X1X2 + c ∑X22
حل المعادلات الثلاث أعلاه ليس بالأمر السهل ولكننا نورد هنا قيم a , b , c مع ملاحظة أن المقام لهم نفس القيمة (باستخدام المحددات) وسنحصل على المعادلة:
Ŷ = a + b X1 + c X2
حيث a , b , c تقديرات لكل من α , β1, β2 على الترتيب
تنويه:
إن a تمثل قيمة ŷ عندما تكون X1 = X2 = 0 في حين تمثل b التغير في ŷ نتيجة تغير X1 بوحدة واحدة بغض النظر عن قيمة X2 ، وتمثل c التغير في ŷ نتيجة تغير X2 بوحدة واحدة بغض النظر عن قيمة X1، وتسمى b , c بمعاملات الانحدار الجزئية.
الحل هنا باستخدام الحاسب الآلي أسرع والأفضل والمثال التالي سيتم حله بأكثر من طريقة