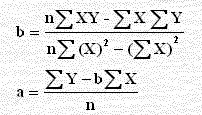
الانحدار غير الخطي البسيط Non Linear Regression الانحدار غير الخطي المتعدد
ذكرنا سابقاً الانحدار الخطي وصورته Y = α + βX وأوجدنا قيم الثوابت وهنا سنبين المعادلة لمنحنى بدل من معادلة الخط المستقيم السابق ذكرها ويعود السبب لمعادلة المنحنى على شكل الانتشار أو نتيجة لخبرة سابقة بأن المتغيرات الموجودة لدينا وهي محل الدراسة علاقات غير الخطية وغالباً تكون في الظواهر الاقتصادية كعلاقة معدل الكلفة بكمية الإنتاج Y = a + b X + c X2 وهي معادلة من الدرجة الثانية حيث a, b , c قيم ثابتة وتعرف بعلاقة الانحدار ألتربيعي والهدف الحصول على أفضل خط انحدار سواء كان خطي أو غير خطي والأفضلية بدءاً للخط المستقيم وإلا نقوم بإضافة تربيع أو تكعيب المتغير المستقل X وإن كنا نعلم مسبقاً بأن المتغيرات لدينا ذات علاقة تربيعية مثلاً فنبدأ باحتسابها وسنتعرض هنا للانحدار غير الخطي البسيط والمتعدد.
الانحدار غير الخطي البسيط Simple Non-Linear Regression
سبق دراسة الانحدار الخطي البسيط Y = a + b X وحسبنا a, b من:
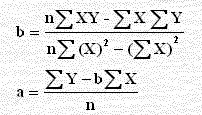
ويختلف غير الخطي البسيط عن الخطي البسيط فيما يلي:
المعامل a الثابت ليس حداً ( كما في Y = a + b X) فظهر بالصورة Y = aXb يمكن تحويلها لخطية (لوغاريتم) أو Y = a bx يمكن تحويلها لخطية (لوغاريتم) أو كمعادلة لوغاريتمي Y = a + LinX كما يمكن بتحويلها لخطية بتغير تعريف المتغيرات فمثلاً Y = aXb بأخذ لوغاريتم الطريفين نحصل على LinY = Lina + b LinX وذلك حسب قوانين الأسس وبوضع LinY = Y , Lina = a , LinX = X نحصل على المعادلة المرادفة Y = a + bX وبالتالي نحسب قيم a , b من:
ويمكن تقدير المتغير بإعادة تعريف المتغيرات كما في المعادلة Y = a + b/X أي Y = a + b(1/x)s وهنا نستخدم نفس القوانين السابقة بوضع s1/X بدل من X أي:
ويمكن تقدير المتغير بإعادة تعريف المتغيرات كالمعادلة Y = a + b LinX وتعرف بالمعادلة نصف اللوغاريتمية باستبدال LinX بدل من s1/X في الصيغ السابقة أي:
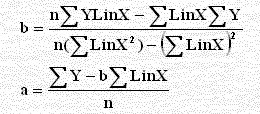
مثال:
الجدول التالي يبين استهلاك 10 عائلات من اللحوم بالكيلوجرام (Y) ومعدل دخلها الشهري بالدينار X والمطلوب تقدير معادلات الانحدار لاستهلاك اللحوم بدلالة الدخل الشهري ثم قدر استهلاك اللحم لعائلة معدل دخلها 250 دينار باستخدام كل من المعادلات المطلوبة.
1) المعادلة الأسية Y = aX b
2) المعادلة العكسية Y = a + b(1/x)s
3) المعادلة نصف اللوغاريتمية Y = a + LinX
4) المعادلة الأسية μy/x = C Dx
| 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | العائلة |
| 300 | 270 | 220 | 200 | 250 | 260 | 255 | 290 | 300 | 250 | الدخل الشهري بالدينار |
| 60 | 50 | 40 | 40 | 55 | 50 | 52 | 44 | 42 | 45 | الاستهلاك بالكيلوجرام |
1) Y = aX b نحولها لمعادلة لوغاريتمية يأخذ اللوغاريتم للطرفين فنحصل على:
LinY = Lin(aX b) = Lin a + Lin(X b) = Lin a + b LinX Then
LinY = Lin a + b LinX
نكون الجدول الشامل للبيانات أعلاه كما يلي
| LinX LinY | LinY | LinX | LinX2 | X2 | الاستهلاك بالكيلوجرام(Y) | الدخل الشهري بالدينار(X) | العائلة |
| 21.0183 | 3.8067 | 5.5215 | 11.0429 | 62500 | 45 | 250 | 1 |
| 21.3189 | 3.7377 | 5.7038 | 11.4076 | 90000 | 42 | 300 | 2 |
| 21.4559 | 3.7842 | 5.6699 | 11.3398 | 84100 | 44 | 290 | 3 |
| 21.8949 | 3.9512 | 5.5413 | 11.0825 | 65025 | 52 | 255 | 4 |
| 21.7535 | 3.9210 | 5.5607 | 11.1214 | 67600 | 50 | 260 | 5 |
| 22.1263 | 4.0073 | 5.5215 | 11.0429 | 62500 | 55 | 250 | 6 |
| 19.5449 | 3.6889 | 5.2983 | 10.5966 | 40000 | 40 | 200 | 7 |
| 19.8964 | 3.6889 | 5.3936 | 10.7873 | 48400 | 40 | 220 | 8 |
| 21.9012 | 3.9120 | 5.5984 | 11.1968 | 72900 | 50 | 270 | 9 |
| 23.3533 | 4.0943 | 5.7038 | 11.4076 | 90000 | 60 | 300 | 10 |
| 214.2635 | 38.5832 | 55.5127 | 111.0254 | 478 | 2595 | Total |
نحسب b , a من الصيغ السابقة
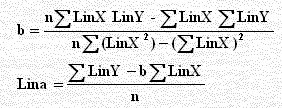
10(214.2635) – (55.5127)(38.5832)
b = ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
10(111.0254) – (55.5127)2
2142.635 – 2141.8576
b = ـــــــــــــــــــــــــــــــــــــــــــــــــ
1110.254 – 3081.6600
0.7774
b = ــــــــــــــــــــــــــــ
– 1971.406
b = – 0.00039 ≈ – 0.0004
38.5832 – (– 0.0004)55.5127)
Lina = ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
10
38.5832 + 0.0222
Lina = ــــــــــــــــــــــــــــــــــــــــــ
10
Lina = 3.8605
a = e3.8605
a = 47.4891 ≈ 47.5
Y = 47.5X– 0.0004 Or LinY = 1.6767 – 0.0004LinX (lin(47.5 = 1.6767)
والاستهلاك المطلوب لعائلة دخلها 250 دينار يكون:
Y = 47.5X– 0.0004
Y = 47.5(250)– 0.0004
Y = 47.5 × 0.9978
Y = 47.3955 ≈ 47
Or
LinY = 1.6767 – 0.0004LinX
LinY = 1.6767 – 0.0004Lin(250)
LinY = 1.6767 – 0.0004× 2.3979
LinY = 1.6767 – 0.0010
LinY = 1.6757
Y = 47.3915 ≈ 47
2) الحل باستخدام المعادلة العكسية:Y = a + b(1/x)s نعوض في الصيغ المبينة أسفل الجدول التالي:
|
(1/X)2 |
(1/X)Y |
1 / X |
الاستهلاك بالكيلوجرام(Y) | الدخل الشهري بالدينار(X) | العائلة |
| 0.000016 | 0.18000 | 0.00400 | 45 | 250 | 1 |
| 0.000011 | 0.14000 | 0.00333 | 42 | 300 | 2 |
| 0.000012 | 0.15172 | 0.00345 | 44 | 290 | 3 |
| 0.000015 | 0.20392 | 0.00392 | 52 | 255 | 4 |
| 0.000015 | 0.19231 | 0.00385 | 50 | 260 | 5 |
| 0.000016 | 0.22000 | 0.00400 | 55 | 250 | 6 |
| 0.000025 | 0.20000 | 0.00500 | 40 | 200 | 7 |
| 0.000021 | 0.18182 | 0.00455 | 40 | 220 | 8 |
| 0.000014 | 0.18519 | 0.00370 | 50 | 270 | 9 |
| 0.000011 | 0.20000 | 0.00333 | 60 | 300 | 10 |
| 0.000156 | 1.85496 | 0.03913 | 478 | 2595 | Total |
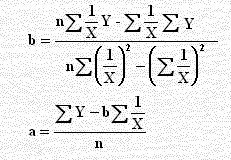
10(1.85496) – (0.03913)(478)
b = ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
10(0.000156) – (0.03913)2
18.5496 – 18.70414
b = ـــــــــــــــــــــــــــــــــــــــــــــــــ
0.00156 – 0.001531
– 0.15454
b = ــــــــــــــــــــــــــــ
0.00003
b = – 5151.3 ≈ – 5151
478 – ( – 5151.3 × 0.03913)
a = ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
10
478 + 201.57
a = ـــــــــــــــــــــــــــــــــــ
10
a = 67.957 ≈ 68
والاستهلاك المطلوب لعائلة دخلها 250 دينار يكون:
Y = 67.957 – 5151.3(1/x)s
Y = 67.957 – (5151.3 ÷ 250)
Y = 67.957 – 20.605
Y = 47.352 ≈ 47.4
3) الحل باستخدام المعادلة نصف اللوغاريتمية:Y = a + b LinXs نعوض في الصيغ المبينة أسفل الجدول التالي:
|
Y LinX |
LinX | LinX2 | X2 | الاستهلاك بالكيلوجرام(Y) | الدخل الشهري بالدينار(X) | العائلة |
| 248.4657 | 5.5215 | 11.0429 | 62500 | 45 | 250 | 1 |
| 239.5589 | 5.7038 | 11.4076 | 90000 | 42 | 300 | 2 |
| 249.4748 | 5.6699 | 11.3398 | 84100 | 44 | 290 | 3 |
| 288.1457 | 5.5413 | 11.0825 | 65025 | 52 | 255 | 4 |
| 278.0341 | 5.5607 | 11.1214 | 67600 | 50 | 260 | 5 |
| 303.6804 | 5.5215 | 11.0429 | 62500 | 55 | 250 | 6 |
| 211.9327 | 5.2983 | 10.5966 | 40000 | 40 | 200 | 7 |
| 215.7451 | 5.3936 | 10.7873 | 48400 | 40 | 220 | 8 |
| 279.9211 | 5.5984 | 11.1968 | 72900 | 50 | 270 | 9 |
| 342.2269 | 5.7038 | 11.4076 | 90000 | 60 | 300 | 10 |
| 2657.1853 | 55.5127 | 111.0254 | 478 | 2595 | Total |
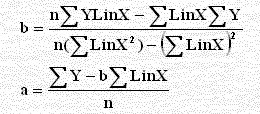
10(2657.1853) – (55.5127)(478)
b = ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
10(111.0254) – (55.5127)2
26571.853 – 26535.0706
b = ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
1110.254 – 3081.6599
36.7824
b = ــــــــــــــــــــــــــــ
– 1971.4059
b = – 0.0187 ≈ – 0.02
478 – ( – 0.0187 × 55.5127)
a = ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
10
478 + 1.0381
a = ـــــــــــــــــــــــــــــــــــ
10
a = 47.9038 ≈ 47.9
والاستهلاك المطلوب لعائلة دخلها 250 دينار يكون:
Y = a + LinX
Y = 47.9 + (– 0.02)(Lin250)
Y = 47.9 – 0.11
Y = 47.8
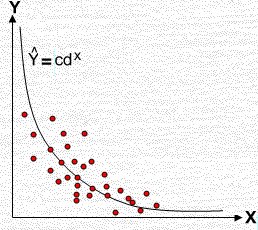
4) الحل باستخدام المعادلة الأسية
أحياناً يكون شكل الانتشار (المبين بالشكل) للبيانات الفعلية دالاً إلى متوسطات μy/x يمكن ضبطها لتمثل بالمنحنى الأسي الذي صيغته μy/x = C Dx حيث أن C, D معاملات يمكن تقديرها من البيانات الفعلية والرمز لتقديرها هو c, d ، وتقدر μy/x بـ Ŷ وتكون معادلة الانحدار الأسية للعينة هي: Ŷ = c dx ولتحويلها لمعادلة خطية نأخذ اللوغاريتم للأساس 10 للطرفين نجد أنَّ:
Log y = Log c + X Log d
بوضع a = Log c , b = Log d فتكون المعادلة:
Log y = a + b X
ولحساب a , b نستخدم الصيغ التالية:
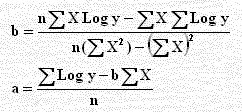
بتكوين جدول البيانات المطلوبة للصيغ السابقة وهو:
|
X Log y |
Log y | X2 | الاستهلاك بالكيلوجرام(Y) | الدخل الشهري بالدينار(X) | العائلة |
| 413.3031 | 1.6532 | 62500 | 45 | 250 | 1 |
| 486.9748 | 1.6233 | 90000 | 42 | 300 | 2 |
| 476.6013 | 1.6435 | 84100 | 44 | 290 | 3 |
| 437.5809 | 1.7160 | 65025 | 52 | 255 | 4 |
| 441.7322 | 1.6990 | 67600 | 50 | 260 | 5 |
| 435.0907 | 1.7404 | 62500 | 55 | 250 | 6 |
| 320.4120 | 1.6021 | 40000 | 40 | 200 | 7 |
| 352.4532 | 1.6021 | 48400 | 40 | 220 | 8 |
| 458.7219 | 1.6990 | 72900 | 50 | 270 | 9 |
| 533.4454 | 1.7782 | 90000 | 60 | 300 | 10 |
| 4356.3154 | 16.7565 | 683025 | 478 | 2595 | Total |
بالتعويض في الصيغ السابقة نجد أن:
10(4356.3154) – (2595)(16.7565)
b = ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
10(683025) – (2595)2
43563.154 – 43483.1175
b = ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
6830250 – 6734025
80.0365
b = ــــــــــــــــــــــــــــ
96225
b = 0.00083 ≈ 0.001 , b = Log d Then d = 1.0019 ≈ 1.002
16.7565 – (0.0008 × 2595)
a = ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
10
16.7565 – 2.1539
a = ــــــــــــــــــــــــــــــــــــــــ
10
a = 1.4681 ≈ 1.5 , a = Log c Then c = 29.3833 ≈ 29.38
المعادلة المطلوبة
Ŷ = c dx
Ŷ = 29.3833(1.0019)X
والاستهلاك المطلوب لعائلة دخلها 250 دينار يكون:
Ŷ = 29.3833(1.0019)250
Ŷ = 47.2275 ≈ 47
والاستهلاك المطلوب لعائلة دخلها 250 دينار يكون:
Log y = a + bX
Log y = 1.4681 + 0.00083×250
Log y = 1.4681 + 0.2075
Log y = 1.6756
Y = 47.3805 ≈ 47