تقدير تباين خط الانحدار Estimate of the Variance of the Regression Line
نستعمل معادلة الانحدار لتقدير قيم Y الفعلية بقيم Ŷ المقدرة للحكم على جودة التقدير بمعرفة مدى مطابقة خط الانحدار على نقاط لوحة الانتشار وذلك بحساب كل من مجموع المربعات الكلي SST ، مجموع المربعات للانحدار SSR ، مجموع المربعات للأخطاء SSE ومنها نحسب تقدير تباين خط الانحدار حيث أن:
مجموع المربعات الكلي SST) Sum of Squares) مثال معامل التحديد الخطأ المعياري لميل الانحدار اختبار فرضية التوزيع الطبيعي
مقياس لتشتت القيم الفعلية حول وسطها الحسابي Y` حيث أن:
SST = ∑ (Yi –`Y )2 Or SST = ∑Y2 – n`Y2
إذا قسمنا SST على درجات الحرية n – 1 نحصل على تقدير للتباين الكلي لقيم Y عن Y`
مجموع المربعات للانحدار SSR) Sum of Squares for Regression)
مجموع مربعات التباين المفسر بواسطة Ŷ = a + b x بين قيم المتغير المستقل والمتغير التابع.
SSR = ∑ (Ŷi –`Y )2 Or SSR = b2[∑xi2 – n`X2] = b[∑xiYi – n`x`Y]
نحصل على قيم Ŷ بالتعويض عن قيمة x في معادلة خط الانحدار ، SSR هو تقدير تباين قيم Ŷ عن الوسط الحسابي لقيم Y الفعلية.
مجموع المربعات للانحدار SSE) Sum of Squares for Errors)
هو عبارة عن مقياس التشتت للقيم الفعلية حول خط الانحدار ويعرف بمجموعات مربعات البواقي.
SSE = ∑ (Y –`Y )2
وهي مجموع مربعات الانحرافات لقيم Y الفعلية عن قيم Y المقدرة.
تباين الخطأ العشوائي:
هو تقدير تباين خط انحدار Y على x ويحسب من الصيغة الرياضية (S2Y/x)
SSE ∑ (Y –`Y )2
S2Y/x = ـــــــــــــــــــــــــــــــ = ـــــــــــــــ
(n – 2) (n – 2)s
الخطأ المعياري لتقدير خط انحدار Y على x هو قيمة الجذر التربيعي لهذا التقدير.
يمكن تكوين جدول تحليل التباين للانحدار كالتالي:
| F المحتسبة | MS | d f | SS | مصدر التغير |
|
μSx / S2Y/x OR MSR / MSE |
MSR =μSx = SSR / 1 |
1 |
∑ ( Ŷi –`Y )2 |
مجموع المربعات بسبب الانحدار SSR |
|
MSE = S2Y/x = SSE / (n – 2) |
n – 2 |
∑ ( Yi – Ŷ )2 |
مجموع مربعات الانحرافات عن الانحدار(البواقي) SSE | |
| n – 1 |
∑ ( Yi –`Y )2 |
مجموع المربعات الكلي SST |
مثال: كون جدول تحليل التباين للانحدار من الجدول الآتي:
الجدول الآتي يبين إنتاج محصول الذرة Y من المساحة المزروعة به X . اختبر معنوية معامل الانحار عند مستوى معنوية 0.05
| Y إنتاج الذرة بالآف الكيلوجرام | X المساحة المزروعة بالهكتار | المنطقة |
| 140 | 50 |
1 |
| 500 | 200 | 2 |
| 400 | 110 | 3 |
| 300 | 80 | 4 |
| 356 | 120 | 5 |
| 240.5 | 74.5 | 6 |
| 200.6 | 88.9 | 7 |
| 33.5 | 5.7 | 8 |
| 69.8 | 11 | 9 |
| 18.7 | 3.2 | 10 |
الحل:
الفرضية الصفرية H0 : β = 0
الفرضية البديلة H1 : β ≠ 0
نكون جدول جديد للحصول على البيانات اللازمة لحساب المطلوب:
|
XY |
X2 | Y2 | Y | X | المنطقة |
| 7000 | 2500 | 19600 | 140 | 50 | 1 |
| 100000 | 40000 | 250000 | 500 | 200 | 2 |
| 44000 | 12100 | 160000 | 400 | 110 | 3 |
| 24000 | 6400 | 90000 | 300 | 80 | 4 |
| 42720 | 14400 | 126736 | 356 | 120 | 5 |
| 17917.25 | 5550.25 | 57840.25 | 240.5 | 74.5 | 6 |
| 17833.34 | 7908.21 | 40240.36 | 200.6 | 88.9 | 7 |
| 190.95 | 32.49 | 1122.25 | 33.5 | 5.7 | 8 |
| 767.8 | 121 | 4872.04 | 69.8 | 11 | 9 |
| 59.84 | 10.24 | 349.69 | 18.7 | 3.2 | 10 |
| 254489.2 | 89017.19(2259.1) | 750760.6 | 2259.1 | 743.3 | Total |
| `Y2 = 51035.3281 | `Y = 225.91 | `X = 74.33 | المتوسط |
باستخدام الصيغ الرياضية نجد أن:
SST = ∑Y2 – n`Y2
= 750760.6 – 10 × 51035.3281
= 750760.6 – 5103.533
= 745657.067
SSR = b[∑xiYi – n`x`Y]
= 2.564[254489.2 – 10 × 74.33 × 225.91]
= 2.564[254489.2 – 167918.903]
= 221966.242
SSE = SST – SSR
= 745657.067 – 221966.242
= 523690.825
| F الجدولية | F المحتسبة | MS | d f | SS | مصدر التغير |
| F0.05,1,9 = 5.12 |
3.391 |
μSx = 221966.242 |
1 |
221966.242 |
مجموع المربعات بسبب الانحدار SSR |
|
S2Y/x = 65461353 |
10 – 2 |
523690.825 |
مجموع مربعات الانحرافات عن الانحدار SSE | ||
|
10 – 1 |
745657.067 |
مجموع المربعات الكلي SST |
ومن حيث F المحتسبة أقل من F الجدولية فنقبل الفرضية الصفرية H0 ونستدل منها على خطية معادلة الانحدار Y = 35.35 + 2.564 X (يراجع المثال) وحال مقاربة أو مساواة β للصفر تكون المعادلة محدودة الكفاءة بقصد التوقع ولذا نبني نموذج غير خطي لوصف العلاقة بين X , Y من خلال إيجاد معامل التحديد (R2) الذي تبين قيمته قوة أو ضعف تفسير التباين بابتعاد قيم Yi عن خط انحدار Ŷ .
R2 = SSR ÷ SST = 221966.242 ÷ 745657.067 = 0.298
يستدل من قيمة معامل التحديد ضعف تفسير التباين.
معامل التحديد The Coefficient of Determination
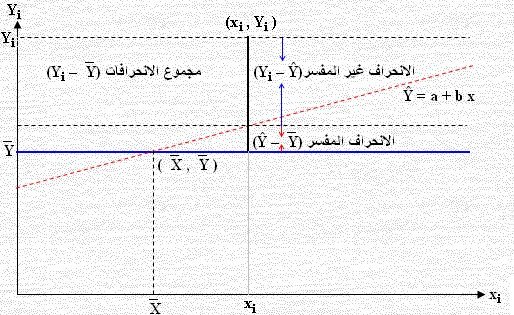
معامل التحديد ورمزه R2 هو قياس وصفي لتفسير الفائدة لمعادلة الانحدار بتقدير القيم ويمثل نسبة انخفاض الأخطاء حال استخدام معادلة الانحدار عوضاً عن استخدام المتوسطات كذلك هو نسبة التباين في القيم الفعلية التي تفسر خط الانحدار وقيمة النسبة هذه SSR / SST حيث أن SSR = SST – SSE إلا أن تأثيره قليل جداً وقيمته بين – 1 ، 1 واقتراب القيمة من 1 يعني فائدة أكثر لمعادلة الانحدار بالتنبؤ لقيمة المتغير التابع وكذلك يكون المتغير المستقل ذو أهمية في تفسير التباين بين القيم الفعلية والشكل التالي يبين مكونات الانحدار الخطي:

من الشكل القيمة الفعلية Yi تنحرف عن خط الوسط Y`بمسافة رأسية تساوي Yi –`Y في حين تنحرف عن خط القيمة المقدرة Ŷ مسافة رأسية Yi – Ŷ
انحراف القيمة المقدرة Ŷ عن خط الوسط Y`يعرف بالانحراف المفسر في حين انحراف القيمة الفعلية (المشاهدة) ن خط الوسط Y`يعرف بالانحراف غير المفسر.
ومن الشكل نجد أن: مجموع الانحرافات = الانحراف المفسر + الانحراف غير المفسر
كما يمكن استخدام الصيغ التالية لحساب كل من SST , SSR , SSE السابق ذكرها أعلاه:
SST = ∑Yi 2 – (∑Yi)2 / n
SSR = b2[∑Xi2 – (∑Xi)2 / n]
SSE = SST – SSR
جدول تحليل التباين للانحدار
| F المحتسبة | MS | d f | SS | مصدر التغير أو مصدر التباين |
|
μSx / S2Y/x OR MSR / MSE |
MSR =μSx = SSR / 1 |
1 |
∑ ( Ŷi –`Y )2 |
مجموع المربعات بسبب الانحدار SSR |
|
MSE = S2Y/x = SSE / (n – 2) |
n – 2 |
∑ ( Yi – Ŷ )2 |
مجموع مربعات الانحرافات عن الانحدار(البواقي) SSE | |
| n – 1 |
∑ ( Yi –`Y )2 |
مجموع المربعات الكلي SST |
الخطأ المعياري لميل الانحدار Standard Error of Regression Slop
في خط الانحدار Y = a + b X الذي ميله b حيث تتراوح قيمته حول قيم المجتمع β ولقياس هذا الانحراف فنقيس الخطأ المعياري لميل الانحدار ويرمز له بالرمز Sb ويحسب من الصيغة الرياضية الآتية حيث Se2 تباين الخطأ العشوائي وهو ثابت لقيم X أو SY/x:
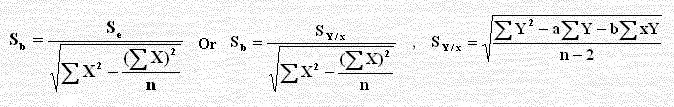
ففي مثالنا السابق نجد أن الخطأ لميل الانحدار(Y = 35.35 + 2.564 X) :

اختبار فرضية التوزيع الطبيعي لمعطيات نموذج الانحدار
يمكن استخدام أحصاءة t لهذا الاختبار والذي صيغته T = (b –β)/Sb مع درجات حرية (n –2) ونبحث الفرضية عند مستوى معنوية α ومقارنة T مع t الجدولية:
الفرضية الصفرية H0 : ß = 0
الفرضية البديلة H1 : ß ≠ 0
ويتم رفض الفرضية الصفرية إذا كان: T ≥ t (n – 2, α/2) or T ≥ –t (n – 2, α/2)s والقيمة صفر تعني لا فرق بين المتغيرات والاختبار هنا ذو طرفين، وبتطبيق ذلك على مثالنا السابق عند مستوى معنوية 0.05 نجد أن:
t0.05,8 = 2.306
T = (b –β)/Sb , ß = 0
= 2.564 / 0.261
= 9.824
> 2.306
نرفض الفرضية الصفرية ونقبل بالفرضية البديلة والدالة على أن قيمة ميل المجتمع تدل على أن معامل الانحدار يختلف عن الصفر