طريقة المربعات الصغرى (Least Square Method)
في المقدمة بينا في الشكل خط انحدار Y على X في حالة العلاقة التامة (معامل الارتباط = 1) ولكن من غير أن تقع جميع نقاط الأزواج على خط الانحدار فإن العلاقة الخطية التامة يجب أن تعدل لتضم الخطأ العشوائي للنقاط التي لا تقع على خط الانحدار بانحرافاتها عن خط الانحدار ويرمز لها لهذا الخطأ بالرمز ε يتصف بالآتي:
1) توزيعه طبيعي 2) وسطه يساوي صفر 3) تباينه ثابت 4) مستقل يمثل انحراف القيم التقديرية عن الحقيقية حسب الصيغة yi = a + bXi + εi
إن تقليل الانحرافات لأصغر
قيمة ممكنة يؤدي لاقتراب قيمة من الصفر عندها نحصل على أفضل خط للانحدار وهو
نادر الحدوث ولذا فإن تلك النقاط التي لا تقع على خط الانحدار تكون قيم
Y الناتجة من التعويض عن قيمة X
( قيمة مشاهدة الموجودة في (x , y) ) ومن حيث أننا أخذنا
خط انحدار لا يمر بهذه النقطة فتوجد قيمة أخرى للمتغير Y
تقابل قيمة X في (x , y) أي
أن قيمة Y تأخذ قيمتين لقيمة X
المناظرة لها إحداها المشاهدة لا تقع على خط الانحدار والمتوقعة الواقعة على خط
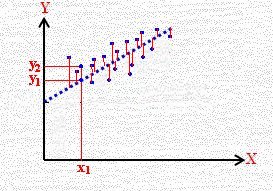
الانحدار (نحصل عليها من الخط المستقيم كما مبين بالشكل بوجد قيمتين
y1 , y2 للقيمة
x1
الزوج (x1 , y2) يمثل النقطة الحقيقية للبيانات الأصلية
الزوج (x1 , y1) يمثل النقطة الواقعة على خط الانحدار (المتوقع أن يكون أفضل خط)
القيمة y1 هي a + bx1 وهي الناتجة من التعويض في المعادلة Y = a + bX بـ x1
توجد نقاط بعدد حجم العينة n كل منها له بعد رأسي عن الخط
انحرافات بين القيمة المشاهدة والقيمة المتوقعة أي (a + bXi) –ـ Yi
القيمة x1 يقابلها بعد رأسي يساوي (a + bx1) –ـ y1 ـ= y1y2 كما مبين بالشكل
هذا الفرق قد يكون سالباً لذا نأخذ مربعات الفروق
نرغب أن تكون أصغر قيمة ممكنة للمقدار الذي يبين مربعات هذه الفروق وهو:
![]()
وهذا ما يعرف بخط المربعات الصغرى ( Least square line ) حيث سيكون حساب a , b مهما معالم خط الانحدار والتي يجب الحصول على قيمها من بيانات العينة اللتان تجعلان مجموع مربعات الانحرافات أقل ما يمكن ويتم الحصول عليهم من المعادلتين الآتيتين بعد تكوين جدول البيات المطلوبة من بيانات العينة:
∑ Y =na + b∑X ................. (1)
∑ XY =a∑ X + b∑X2 .........(2)
توجد أكثر من طريقة لحل المعادلتين السابقتين مثل الحذف أو التعويض أو المحددات أو المصفوفات أو الرسم البياني أو التفاضل وكلها تؤدي للحصول على قيمتي a , b ومنها نحصل على معادلة خط الانحدار وبحل المعادلتين يتم الحصول على قيم a , b وهنا تجد:

هناك صيغتان لحساب a الأولى بقسمة Y∑Y = na + b∑Xعلى n والثانية من قانون الوسط الحسابي وهما
