
التوزيع المعتدل (الطبيعي) Normal Distribution المئينات Percentile الدرجة الزائية الدرجة التائية جدول Z الأمثلة
يرتبط هذا التوزيع بمتغير عشوائي متصل وهو دالة في المتغير العشوائي ويمكن تمثيله بيانياً وهو من أهم التوزيعات الاحتمالية لتمثيله العديد من الظواهر وهو المناسب لها سواء كانت القيم التي تحدث في الظاهرة كبيرة جداً أو صغيرة جداً باحتمالات صغيرة.
هو توزيع مستمر يعرف أيضاً بتوزيع جاوس (كارل جاوس) حيث جرى نشره سنة 1733م ويعتبر المتغير المعتدل عشوائي مستمر لكونه يتكون من عدد لانهائي من القيم الحقيقية والتي يمكن ترتيبها على مقياس متصل، وهو من أهم التوزيعات في علم الإحصاء بل يعتبر أساساً لكثير من النظريات الإحصائية الرياضية ويلعب دوراً أساسياً في اختبارات الفروض الإحصائية وفترات الثقة وغير ذلك وأن الكثير من الصفات كالطول والوزن ومستوى الذكاء والزواج وما إلى ذلك إذا قيست ولعدد كبير من المشاهدات فإن توزيعها يقترب من التوزيع الطبيعي إن لم يكن يأخذ صورة التوزيع الطبيعي، ويعرف بأسماء مختلفة منها التوزيع ألجرسي لكون شكله يشبه ألجرس.
خصائص التوزيع المعتدل:
1) منحنى التوزيع المعتدل متصل (مستمر) منحناه (Normal Curve) يشبه شكل الجرس ويمتد ذراعه من – ∞ إلى ∞ .
معادلته الرياضية في الفترة ] – ∞ ، ∞ [ هي:

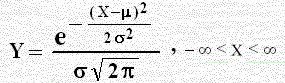
بإجراء تكامل Y على الفترة ] – ∞ ، ∞ [ نحصل على المساحة تحت المنحنى وفوق المحور الأفقي، والتمثيل البياني له كما مبين بالشكل المقابل وكل نقطة من نقاط المنحنى تمثل قيمة لدالة تعرف بدالة كثافة الاحتمال (Probability density function) عند هذه النقطة والاحتمال هنا أي في التوزيع المستمر هو قيمة المساحة تحت منحنى دالة الكثافة المناظرة لفترة وليس لنقطة فالمساحة باللون الأصفر والمحصورة بين المنحنى والمحور الأفقي والمستقيمان x1 = a , x2 = b تساوي احتمال المتغير العشوائي المستمر X أي قيمة في الفترة [ a , b] هذا وأن المساحة الكلية الواقعة بين منحى التوزيع المعتدل والخط الأفقي تساوي الواحد الصحيح وهي ما تعرف بالمساحة تحت المنحنى = 1 ولمعرفة احتمال وقوع x بين x1 و x2 نحسب تكامل الدالة السابقة من x1 إلى x2 ، مع ملاحظة أن احتمال أي حدث P(A)s يقع بين الصفر والواحد الصحيح أي أن: 1s>sP(A)s>s0
2) المنحنى متماثل حول الخط الرأسي (العمود النازل من أعلى نقطة للمنحنى على الخط الأفقي) وإن التماثل يعني بأن صورة الشكل على أحد جانبي محور التماثل هي الجزء الواقع على الجانب الأخر وموقع العمود على الخط الأفقي يمثل قيمة الوسط الحسابي أي أن المنحنى متماثل حول وسطه الحسابي أو حول المستقيم x = μ ، وان μ هي
القيمة المتوقعة ويصل المنحنى لقيمته العظمى عند X = μ
3) المنحنى ممتد من – ∞ إلى + ∞ ولا يلتقي بالمحور الأفقي.
4) للمنحنى المعتدل معلمتين هما الوسط الحسابي والانحراف المعياري معتمد كلياً عليهم فاختلاف الوسط أو الانحراف المعياري لتوزيعين معتدلين يعني اختلاف في الشكل أو
اختلاف في المركز كما مبين بالشكل الآتي ولكل زوج ( μ ، σ ) للوسط والانحراف المعياري منحنى توزيع مختلف وبالتالي تختلف المساحة تحت المنحنى لكل منحنى ولذا
أخذنا ( 0 ، 1) كتوزيع معياري يسمى التوزيع الطبيعي المعياري متغيره العشوائي هو Z السابق ذكرها، وهنا جدول خاص بها.
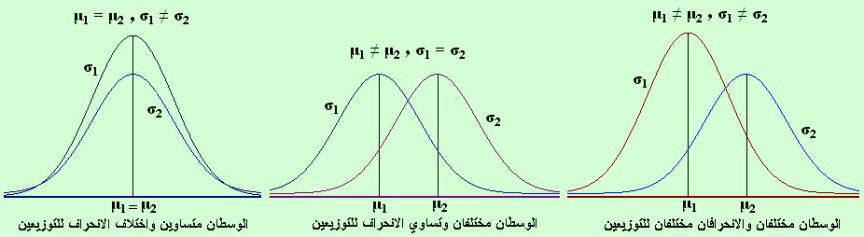
5) للمنحنى قمة واحدة أي له منوال واحد وبالتالي فالمنحني وحيد المنوال
6) المتوسطات الثلاثة متساوية (الوسط والوسيط والمنوال) بالنسبة للمتغير العشوائي المعتاد.
7) المساحة الواقعة تحت المنحنى والمحصورة بالمستقيمين:
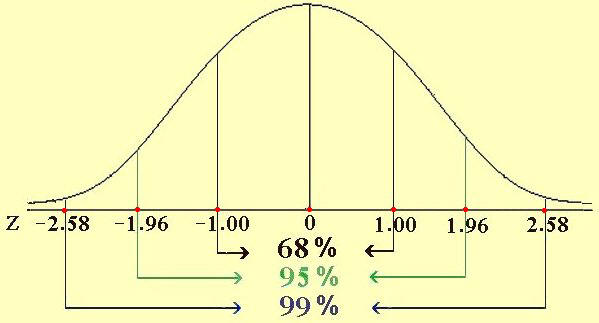
x = μ – σ و x = μ + σ تساوي 68.26% تقريباً من المساحة الكلية تحت المنحنى أي 68.26% من قيم المتغير العشوائي المعتاد تقع في [μ + σ ، μ – σ]
x = μ – 2σ و x = μ + 2σ تساوي 95.45% تقريباً من المساحة الكلية تحت المنحنى أي 95.45% من قيم المتغير العشوائي المعتاد تقع في [μ + 2σ ، μ – 2σ]
x = μ – 3σ و x = μ + 3σ تساوي 99.73% تقريباً من المساحة الكلية تحت المنحنى أي 99.73% من قيم المتغير العشوائي المعتاد تقع في [μ + 2σ ، μ – 2σ]
أي أن وقوع أي مفردة على بعد 1، 2، 3 انحرافات معيارية (s1s, 2s, 3s) من الوسط الحسابي هي القيم السابقة كما مبين بالشكل الآتي:
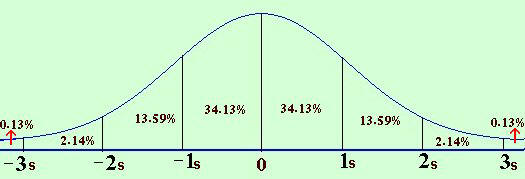
لاحظ أن 34.19% من المساحة تحت المنحنى التي تساوي الواحد الصحيح أي 0.3413 ، وبجمع القيم المبينة في الرسم أعلاه نجد أنها تساوي الواحد الصحيح تقريباً.
إن هذه القيم ما هي إلا احتمالات للقيم كمساحة تحت المنحنى ولأي دالة احتمال يكون مجموع احتمالاتها البسيطة يساوي الواحد الصحيح ونقصد في الأصل المساحة هنا لمساحة الأعمدة للقيم ولكن من الصعب رسم كل الأعمدة وعرض احتمال كل منها ولذا استعضنا عنها باحتمالاتها.
0.0013 + 0.0214 + 0.1359 + 0.3413 + 0.3413 + 0.1359 + 0.0214 + 0.0013 = 0.9998 ≈ 1
والتوزيع الطبيعي المعياري (Standard Normal Distribution) الذي وسطه صفر وانحرافه المعياري 1 متغيره العشوائي المعياري Z بالصيغة السابق ذكرها، ومنحناه كما مبين أعلاه ويمكن حذف s من القيم على الخط الأفقي وقد نضع قيم x والمناظرة لها Z على الخط الأفقي إن دعت الحاجة.
وقد أمكن إيجاد جدول لتوزيع معتدل معياري لقياس جميع التوزيعات المعتادة (اعتدالي) من خلال النظرية التالية:
إذا كانت x متغير عشوائي له توزيع اعتدالي بتوقع μ وتباين σ2 حيث σ الانحراف المعياري فإن: Z = (x – μ)÷σ له توزيع اعتدالي وسطه صفر وانحرافه المعياري واحد صحيح ويعرف بالتوزيع المعتدل المعياري وله جداول لقيم دالة التوزيع الاحتمالي ولقيم دالة كثافة الاحتمال لأي قيمة من قيم المتغير العشوائي، ويعرف المنحنى هنا بالمنحنى الطبيعي القياسي خطه الأفقي مقسم لدرجات Z كما مبين بالشكل التالي والذي يبين أيضاً المساحة تحت المنحنى وقد قسمت لدرجات معيارية حسب قيم Z حيث قيم x تناظرها قيم Z تحسب من الصيغة الرياضية السابقة أو من الصيغة: Z = ( x –`X ) ÷ s حيث s الانحراف المعياري وأن القيمة Z قيمة معيارية وهي الفرق بين القيمة المشاهدة والوسط الحسابي معبراً عنها بوحدات معيارية بمعنى أكثر دقة قيمة Z عبارة عن عدد الوحدات المعيارية (الانحراف المعياري) التي تفصل بين قيمة x والوسط الحسابي.
وهناك خواص أخرى من بينها إذا كان Ln(x)s توزيع طبيعي فإن x توزيع طبيعي وستذكر الأخرى في حينها والخاصة بتوزيع ذات الحدين وتوزيع χ2 .
يمكن صياغة معادلة المنحنى بدلالة Z على الصورة الآتية حيث أن Y تمثل كثافة قيم المتغير الطبيعي المعياري أو التكرارات للمنحنى.
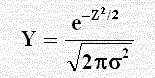
يمكن تحويل قيمة المتغير المعتدل x لمتغير معتدل معياري Z من الصيغة السابقة فمثلاً إذا كان لدينا توزيع اعتدالي وسطه 150 درجة وانحرافه المعياري 90 درجة فيمكن باستخدام الصيغة السابقة حساب قيمة x = 270 نستخدم الصيغة السابقة أي أن:
Z = ( 270 – 90) ÷ 90 = 2
بالرجوع لجدول Z نجد أن المساحة تحت المنحنى التي تقابل Z = 2 تساوي 0.9772 (المساحة التي تقع على يسار العدد 2 (الشكل كل السابق)، وتحسب بطريقتين:
الأولى : المساحة = 1 – (0.0013 + 0.0214) = 1 – 0.0227 = 0.9773
الثانية : المساحة = 0.0013 + 0.0214 + 0.1359 + 0.3413 + 0.3413 + 0.1359 = 0.9771
المئين مفرد مئينات أو الدرجة المئينية هو نقطة على توزيع تكراراته نسب مئوية من مجموع كلي(تقسيم التوزيع إلى مائة جزء متساوٍ)، والهدف هنا تحويل الدرجة الخام لدرجة أخرى يسهل عملية المقارنة، والمئين هو درجة تقل عنها أو تقابلها نسبة مئوية من الأفراد( المركز النسبي للفرد في مجموعته).
وببساطة يمكن القول بأن طالب في الصف الثالث ثانوي ب حصل على 752 درجة من أصل المجموع الكلي للدرجات (1000درجة) وبمقارنته مع طلاب صفه (25 طالب) كان ترتيبه على الصف السادس عشر (16) وهنا لدينا القيمة 752 وتمثل مجموع درجات الطالب ، العدد 16 الدال على ترتيب الطالب في الصف أي هو أفضل من 15 طالب في الصف أو أن هناك 9 طلاب أفضل منه أي حصلوا على مجموع يزيد عن 752 درجة، نود أن نقول بأنه يجب التمييز بين القيمة 752 كدرجات والقيمة 16 كترتيب أو يجب أن نفرق بين قيمة المئين وترتيب المئين والعدد 16 الدال على الترتيب يعني هنا 16 ×100 ÷ 25 = 64% تعني أن القيمة 752 يقابلها المئين 64 والذي يعني أن 64% من الطلاب حصلوا على درجة 752 أو أقل منها من طلاب الصف أو تعني أن 36% [(1 – 64)%] حصلوا على درجة أكبر من 752 ( 9 × 100 ÷ 25 = 36%).
على العموم إذا قلنا أن شخصاً ضمن مجموعة ما حصل على مئين قدره 74 فنستدل من ذلك بأن هذا الشخص تفوق على 74% من أفراد هذه المجموعة أو هذا الشخص تفوق عليه 26% من أفراد مجموعته هذه أو أن هذا الشخص من أفضل 26% من أفراد هذه المجموعة.
لكل درجة مئينية رتبة والعكس صحيح، ولذا فإن الدرجة المئينية تبين موضع الشخص (الفرد) النسبي ضمن توزيع معين، ويجب التنبيه بعدم صحة القول درجة الشخص تساوي المئين 90 تعني بأنه حصل على 90 درجة من 100 ولكن يمكن القول بأن صاحب المئين 90 أفضل من صاحب المئين 85 كما انه لا وجود لمئين أكبر من 100 وكذلك لا يقل المئين عن الصفر أي أن المئين قيمه تتراوح بين 0 ، 100 أي صفر ≤ قيمة المئين ≤ 100
الرتبة المئينية لا تعني قيمتها بمعنى الرتبة المئينية 95 مثلاً لا تعني بأن صاحبها متفوق فقد يكون ضمن مجموعة متخلفين عقلياً والعكس الرتبة المئينية 12 لا تعنى ضعف مستوى صاحبها فقد يكون ضمن مجموعة من الأذكياء وهذا يقودنا لأخذ الحيطة عند مقارنة المئينات وخاصة عند اختلاف المجموعات المرجعية ولكن من السهولة للمقارنة ضمن المجموعة الواحدة وهو ما نريده ويمكن حساب الرتبة المئينية للدرجة وبالعكس حسابياً أو بيانياً ــ راجع هنا أمثلة على المئين و ..ــ
تستخدم المئينات كشكل من أشكال التقسيمات المعيارية فتوجد علاقة بين الرتبة المئينية والدرجة المعيارية الزائية (Z) فقولنا أن رتبة المئين للدرجة 65 هي 20 ويرمز لها PR65 = 20 تعني وجود 20% من الدرجات أقل من 65 أو ما نسبته 20% من المساحة تحت المنحنى للتوزيع المعتدل للعلامة Z التي تقابل 65 درجة.
مثال (1) أوجد احتمال X > 200 لتوزيع طبيعي وسطه الحسابي 150 وانحرافه المعياري 28 حساب Z,T باستخدام SPSS
الحل: نحول القيمة 200 (توزيع طبيعي) لقيمة معيارية (Z) حسب الصيغة السابقة
Z = (x – μ)÷σ
= (200 – 150) ÷ 28
= 50 ÷ 28
= 1.79
P( X > 200) = P( Z > 1.79)
= 1 – P( Z < 1.79) من الجدول نجد أن 1.79 يقابلها القيمة 0.9633
= 1 – 0.9633
= 0.0367 ≈ 0.04
مثال (2) أوجد احتمال X < 200 لتوزيع طبيعي وسطه الحسابي 150 وانحرافه المعياري 28
الحل: كما في المثال (1) نحول القيمة 200 لقيمة معيارية (Z) حسب الصيغة السابقة
Z = (x – μ)÷σ
= (200 – 150) ÷ 28
= 50 ÷ 28
= 1.79
القيم في الجدول تعبر عن المساحة على يسار القيمة الزائية أي التي أقل من قيمة X ومن الجدول نجد أن 1.79 يقابلها القيمة 0.9633 (1.7 العمود الأول ، 0.09في الصف الأول)وهو قيمة الاحتمال المطلوب (0.96) أي أن:
P( X < 200) = 0.9633 ≈ 0.96
لاحظ أن مجموع الاحتمالين في المثالين السابقين يساوي الواحد الصحيح ( 0.96 + 0.04 = 1) لكونهم اشتمالا على المساحة تحت المنحنى كاملة.
مثال (3) : في توزيع طبيعي لأوزان طلاب مدرسة ثانوية عددهم 500 طالب، وكان وسطهم الحسابي (الأوزان) يساوي 62 كجم والانحراف المعياري يساوي 4 ، أوجــد عــدد
الطلبة التي تنحصر أوزانهم بين 55 ، 65 كجم
الحــل : سنحسب المساحة تحت منحنى التوزيع الطبيعي بتحويل القيم 55 ، 65 لقيم معيارية (Z) باستخدام Z = (x – μ)÷σ
Z = (x – μ)÷σ , x = 65 , μ = 62 , σ = 4
= (65 – 62) ÷ 4
= 3 ÷ 4
= 0.75
من الجدول نجد أن: 0.75 تقابل القيمة 0.7734 (0.7 في العمود الأول ، 0.05 في الصف الأول)
Z = (x – μ)÷σ , x = 55 , μ = 62 , σ = 4
= (55 – 62) ÷ 4
= – 7 ÷ 4
= – 1.75
من الجدول نجد أن: 1.75 تقابل القيمة 0.9599 (1.7 في العمود الأول ، 0.05 في الصف الأول)
ومن حيث أن القيمة سالبة فإن – 1.75 تعطي مساحة = 1 – 0.9599 = 0.0401
الاحتمال = المساحة تحت المنحنى بين Z = 1.75 ، Z = – 1.75 أي 0.7734 – 0.0401 = 0.7333
عدد الطلبة المطلوب = 500 × 0.7333 ≈ 367
لاحظ أن : احتمال الحدث أ = عدد حالات وقوع أ بالفعل ÷ عدد الحالات التي يمكن أن يقع فيها أ ، عدد الحالات الكلية هنا 500 ، الاحتمال المستخرج = 0.7333
المئين X يعني المساحة تحت المنحنى وهذه يقابلها قيمة Z مثل المئين 62 يعني المساحة تحت المنحنى 0.62 وتقابل قيمة Z فمن الجدول تساوي 0.31
جدول Z حيث النتائج التالية من التعويض (برنامج EXCEL) عن قيم Z في القانون التالي:
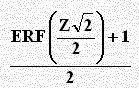
| Z | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
| 0.0 | 0.5000 | 0.5040 | 0.5080 | 0.5120 | 0.5160 | 0.5199 | 0.5239 | 0.5279 | 0.5319 | 0.5359 |
| 0.1 | 0.5398 | 0.5438 | 0.5478 | 0.5517 | 0.5557 | 0.5596 | 0.5636 | 0.5675 | 0.5714 | 0.5753 |
| 0.2 | 0.5793 | 0.5832 | 0.5871 | 0.5910 | 0.5948 | 0.5987 | 0.6026 | 0.6064 | 0.6103 | 0.6141 |
| 0.3 | 0.6179 | 0.6217 | 0.6255 | 0.6293 | 0.6331 | 0.6368 | 0.6406 | 0.6443 | 0.6480 | 0.6517 |
| 0.4 | 0.6554 | 0.6591 | 0.6628 | 0.6664 | 0.6700 | 0.6736 | 0.6772 | 0.6808 | 0.6844 | 0.6879 |
| 0.5 | 0.6915 | 0.6950 | 0.6985 | 0.7019 | 0.7054 | 0.7088 | 0.7123 | 0.7157 | 0.7190 | 0.7224 |
| 0.6 | 0.7257 | 0.7291 | 0.7324 | 0.7357 | 0.7389 | 0.7422 | 0.7454 | 0.7486 | 0.7517 | 0.7549 |
| 0.7 | 0.7580 | 0.7611 | 0.7642 | 0.7673 | 0.7704 | 0.7734 | 0.7764 | 0.7794 | 0.7823 | 0.7852 |
| 0.8 | 0.7881 | 0.7910 | 0.7939 | 0.7967 | 0.7995 | 0.8023 | 0.8051 | 0.8078 | 0.8106 | 0.8133 |
| 0.9 | 0.8159 | 0.8186 | 0.8212 | 0.8238 | 0.8264 | 0.8289 | 0.8315 | 0.8340 | 0.8365 | 0.8389 |
| 1.0 | 0.8413 | 0.8438 | 0.8461 | 0.8485 | 0.8508 | 0.8531 | 0.8554 | 0.8577 | 0.8599 | 0.8621 |
| 1.1 | 0.8643 | 0.8665 | 0.8686 | 0.8708 | 0.8729 | 0.8749 | 0.8770 | 0.8790 | 0.8810 | 0.8830 |
| 1.2 | 0.8849 | 0.8869 | 0.8888 | 0.8907 | 0.8925 | 0.8944 | 0.8962 | 0.8980 | 0.8997 | 0.9015 |
| 1.3 | 0.9032 | 0.9049 | 0.9066 | 0.9082 | 0.9099 | 0.9115 | 0.9131 | 0.9147 | 0.9162 | 0.9177 |
| 1.4 | 0.9192 | 0.9207 | 0.9222 | 0.9236 | 0.9251 | 0.9265 | 0.9279 | 0.9292 | 0.9306 | 0.9319 |
| 1.5 | 0.9332 | 0.9345 | 0.9357 | 0.9370 | 0.9382 | 0.9394 | 0.9406 | 0.9418 | 0.9429 | 0.9441 |
| 1.6 | 0.9452 | 0.9463 | 0.9474 | 0.9484 | 0.9495 | 0.9505 | 0.9515 | 0.9525 | 0.9535 | 0.9545 |
| 1.7 | 0.9554 | 0.9564 | 0.9573 | 0.9582 | 0.9591 | 0.9599 | 0.9608 | 0.9616 | 0.9625 | 0.9633 |
| 1.8 | 0.9641 | 0.9649 | 0.9656 | 0.9664 | 0.9671 | 0.9678 | 0.9686 | 0.9693 | 0.9699 | 0.9706 |
| 1.9 | 0.9713 | 0.9719 | 0.9726 | 0.9732 | 0.9738 | 0.9744 | 0.9750 | 0.9756 | 0.9761 | 0.9767 |
| 2.0 | 0.9772 | 0.9778 | 0.9783 | 0.9788 | 0.9793 | 0.9798 | 0.9803 | 0.9808 | 0.9812 | 0.9817 |
| 2.1 | 0.9821 | 0.9826 | 0.9830 | 0.9834 | 0.9838 | 0.9842 | 0.9846 | 0.9850 | 0.9854 | 0.9857 |
| 2.2 | 0.9861 | 0.9864 | 0.9868 | 0.9871 | 0.9875 | 0.9878 | 0.9881 | 0.9884 | 0.9887 | 0.9890 |
| 2.3 | 0.9893 | 0.9896 | 0.9898 | 0.9901 | 0.9904 | 0.9906 | 0.9909 | 0.9911 | 0.9913 | 0.9916 |
| 2.4 | 0.9918 | 0.9920 | 0.9922 | 0.9925 | 0.9927 | 0.9929 | 0.9931 | 0.9932 | 0.9934 | 0.9936 |
| 2.5 | 0.9938 | 0.9940 | 0.9941 | 0.9943 | 0.9945 | 0.9946 | 0.9948 | 0.9949 | 0.9951 | 0.9952 |
| 2.6 | 0.9953 | 0.9955 | 0.9956 | 0.9957 | 0.9959 | 0.9960 | 0.9961 | 0.9962 | 0.9963 | 0.9964 |
| 2.7 | 0.9965 | 0.9966 | 0.9967 | 0.9968 | 0.9969 | 0.9970 | 0.9971 | 0.9972 | 0.9973 | 0.9974 |
| 2.8 | 0.9974 | 0.9975 | 0.9976 | 0.9977 | 0.9977 | 0.9978 | 0.9979 | 0.9979 | 0.9980 | 0.9981 |
| 2.9 | 0.9981 | 0.9982 | 0.9982 | 0.9983 | 0.9984 | 0.9984 | 0.9985 | 0.9985 | 0.9986 | 0.9986 |
| 3.0 | 0.9987 | 0.9987 | 0.9987 | 0.9988 | 0.9988 | 0.9989 | 0.9989 | 0.9989 | 0.9990 | 0.9990 |