إيجاد الرتبة المئينية لدرجة وبالعكس من جدول تكراري
إيجاد الرتبة المئينية لدرجة وبالعكس من منحنى تكراري متجمع نسبي
الجدول التكراري الآتي يبين درجات مجموعة من الطلاب:
|
الفئات Intervals |
الحدود العليا الفعلية Exact upper limit |
التكرار F |
التكرار المتجمع الصاعد CF |
التكرار النسبي / المئوي FR |
التكرار المتجمع المئوي RCF |
| 80-84 | 84.5 | 3 | 3 | ( 3 ÷ 110 ) × 100 = 2.727 | 3 |
| 85-89 | 89.5 | 5 | 8 | 4.545 | 7 |
| 90-94 | 94.5 | 5 | 13 | 4.545 | 12 |
| 95-99 | 99.5 | 4 | 17 | 3.636 | 15 |
| 100-104 | 104.5 | 12 | 29 | 10.909 | 26 |
| 105-109 | 109.5 | 14 | 43 | 12.727 | 39 |
| 110-114 | 114.5 | 17 | 60 | 15.455 | 55 |
| 115-119 | 119.5 | 13 | 73 | 11.818 | 66 |
| 120-124 | 124.5 | 9 | 82 | 8.182 | 75 |
| 125-129 | 129.5 | 9 | 91 | 8.182 | 83 |
| 130-134 | 134.5 | 7 | 98 | 6.364 | 89 |
| 135-139 | 139.5 | 5 | 103 | 4.545 | 94 |
| 140-144 | 144.5 | 3 | 106 | 2.727 | 96 |
| 145-149 | 149.5 | 2 | 108 | 1.818 | 98 |
| 150-154 | 154.5 | 2 | 110 | 1.818 | 100 |
| Total | 110 |
التمثيل البياني للعمودين الحدود العليا الفعلية ، RCF مبين أدناه
لمعرفة الرتبة المئينية حسابياً للدرجة i116 مثلاً فهي تقع في عمود الحدود العليا للفئات بين i114.5 او i119.5 اللذين يقابلان i73 ، 60 في عمود التكرار المتجمع الصاعد وعودة لكيفية حساب الوسيط لنتبع نفس الطريقة حيث القانون

وعليه يكون: i5 (فرق i114.5عن i119.5) لها i13 (فرق i60 عن i73) وعندنا i116 تبعد عن i114.5مسافة i1.5 فكم لها ؟ أي
i13 ← 5
i1.5← ؟
؟ = i13 × 1.5 ÷ 5 = 3.9 ، تضاف لبداية الفئة i60فنحصل على i63.9وتكون:
![]()
والعكس إذا كان لدينا درجة X رتبتها المئينية = i58ونريد معرفة قيمة الدرجة، نوجد قيمة i58في التكرار المتجمع أي :
التكرار المتجمع للدرجة = الرتبة المئينية × التكرار الكلي ÷ i100
= i58 × 110 ÷ 100 = 63.8
وهي (i (63.8 تقع بين i73 ، 60 التي يقابلها i119.5 ، 114.5 (الحدود الفعلية العليا)، وباستخدام النسبة والتناسب نجد أن:
i5 (فرق i114.5عن i119.5) لها i13 (فرق i60 عن i73) وعندنا i63.8تبعد عن i60مسافة i3.8 فكم لها ؟ أي
i 5 ← 13
i3.8 ← ؟
؟ ≈ i5× 3.8 ÷ 13 = 1.5 ، تضاف لبداية الفئة i114.5فنحصل على i116وتكون الدرجة المطلوبة X هي i116.
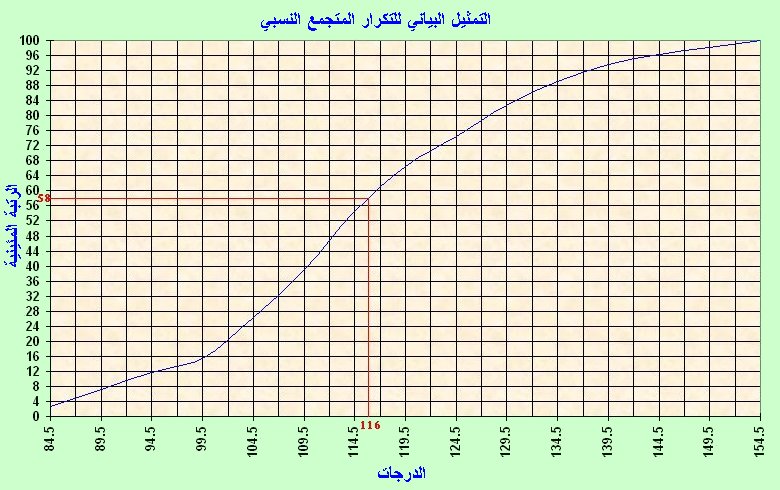
الحسابات من الرسم البياني:
من الرسم البياني كما في الشكل الآتي نعين القيمة i116على المحور الأفقي ونقيم منها عمود يلاقي المنحنى في نقطة نسقط منها عمود على المحور الرأسي فنجد القيمة i58التي هي المئين للدرجة i116، وبالعكس إذا رسمنا خط موازي الخط الأفقي من الرتبة i58ليلاقي المنحنى في نقطة نسقط منها عمود على الخط الأفقي لنجد الدرجة i116كما هو مبين بالشكل الآتي: