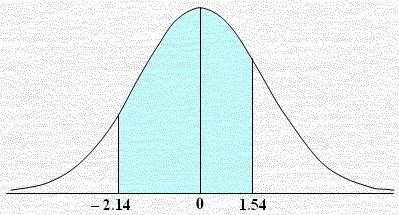
التوزيع الإحصائي الطبيعي
توزيع متصل له شكل الناقوس.
تتساوى فيه مقاييس النزعة المركزية الوسط والوسيط والمنوال.
متماثل حول وسطه (صفر).
الانحراف المعياري له يساوي الواحد الصحيح.
طرفاه يمتدان إلى مالا نهاية دون أن يلتقيا المحور الأفقي.
المساحة أسفله وفوق المحور الأفقي تساوي الواحد الصحيح.
معياري بمعنى أنه يمكن مقارنة أشياء مختلفة.
الالتواء و التفلطح صفر.
يحمل نسب متساوية وثابتة من الوسط فجهة اليمين (يمين الوسط) موجبه ويسارها سالبه.
كافة الملاحظات المذكورة هي خارج الحل وللتوضيح بدل من ذكر أمثلة أخرى
مثال(2) مثال(3) مثال(4) مثال(5) مثال(6) مثال(7) مثال(8) مثال(9) مثال(10)
مثال(1):
احسب المساحة المحصورة بين i– 2.14 , 1.54والواقعة تحت منحنى التوزيع الطبيعي والمبينة بالشكل المرفق.
الحـل:
نعلم أن العدد i1.54يقابله في جدول Z قيمة المساحة الواقعة يساره وكذلك العدد i– 2.14 تقابله مساحة في جدول Z والفرق بين المساحتين يعطينا المساحة المطلوبة.
مع ملاحظة حسابنا للقيمة السالبة بموجبها مطروح من الواحد الصحيح. جدول Z
| العدد | المساحة |
| 1.54 | 0.9382 |
| – 2.14 | 1 – 0.9838 = 0.0162 |
المساحة المطلوبة = i0.9382 – 0.0162
= i0.9220
أو بجمع القيم الجدولية للقيمتين مباشرة بحذف i0.5000 من قيمها الجدولية أي (i (0.9838 – 0.5000) , i (0.9382 – 0.5000
المساحة المطلوبة = i0.4382 + 0.4838
= i0.9220
تنويه: جدول z يقرأ المساحة على يسار العدد وعليه نقول
المساحة على يمين العدد 1.54 = 1 – 0.9832 = 0.0168
المساحة على يمين العدد صفر هي 0.5
احسب المساحة بين Z = – 1.5 , Z = – 0.43
الحـل:
المساحة المطلوبة = المساحة على يسار –0.43 مطروحاً منها المساحة على يسار –1.5
= (1 – 0.6664) – (1 – 0.9332)
= 0.3336 – 0.0668
= 0.2668
أو
P(– 0.43 > Z > – 1.5)= [1– P(Z < 0.43)] – [1 – P(Z < 1.5)]
= (1 – 0.6664) – (1 – 0.9332)
= 0.3336 – 0.0668
= 0.2668
احسب المساحة بين Z = 1.5 , Z = 0.43
الحـل:
المساحة المطلوبة = المساحة على يسار1.5 مطروحاً منها المساحة على يسار0.43
= 0.9332 – 0.6664
= 0.2668
أو
P( 0.43 < Z < 1.5)= P(Z < 1.5) – P(Z < 0.43)
= 0.9332 – 0.6664
= 0.2668
إذا كانت مجموعة مكونة من 400 عضو في نادي تتوزع توزيعاً طبيعياً في العمر بمعدل 40 سنة بانحراف معياري قدره 5 فاحسب:
1) عدد الأعضاء الذين أعمارهم بين 35 إلى 45 سنة.
2) عدد الأعضاء الذين أعمارهم أقل من 50
3) عدد الأعضاء الذين أعمارهم أقل من 35 واكبر من 45
الحـل:
1) نحسب قيمة Z من القانون للعمر 35:
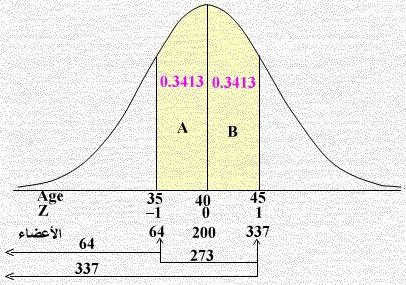
Z = ( X – μ ) ÷ σ = ( 35 – 40) ÷ 5 = – 1
 القيمة الجدولية
المقابلة للعدد –
1 (المساحة ) هي 1–
0.8413 = 0.1587
القيمة الجدولية
المقابلة للعدد –
1 (المساحة ) هي 1–
0.8413 = 0.1587
" لاحظ عدد الأعضاء هنا = 0.1587 × 400 ≈ 64 "
" لاحظ أن العدد 0.1587 هو احتمال عمر العضو أقل من 35 سنة "
" لاحظ مساحة المنطقة الصفراء A = 0.5 – 0.1587 = 0.3413 "
نحسب قيمة Z من القانون للعمر 45:
Z = ( X – μ ) ÷ σ = ( 45 – 40) ÷ 5 = 1
القيمة الجدولية المقابلة للعدد 1(المساحة ) هي 0.8413
ويمكن حسابها من –1 السابقة وهي 1 – 0.1587 = 0.8413
" لاحظ عدد الأعضاء هنا = 0.8413 × 400 ≈ 337 "
" لاحظ أن العدد 0.8413 هو احتمال عمر العضو أقل من 45 سنة "
" لاحظ مساحة المنطقة الصفراء B = 0.8413 – 0.5 = 0.3413 "
الفرق بين المساحتين = 0.8413 – 0.1587 = 0.6826 أو مجموعهم كما مبين بالشكل
المطلوب = 0.6826 × 400 ≈ 273 عضو
" من الملاحظتين أعلاه عدد الأعضاء = 337 – 64 = 273 "
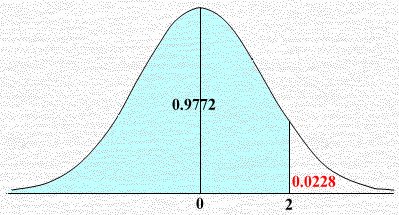
2) نحسب قيمة Z من القانون للعمر 50:
Z = ( X – μ ) ÷ σ = ( 50 – 40) ÷ 5 = 2
القيمة الجدولية المقابلة للعدد 2 ( المساحة) هي 0.9772على يسار القيمة 2
فيكون عدد الذين تقل أعمارهم عن 50 = 0.9772 × 400 ≈ 381 عضو
لاحظ:
الذين يزيد أعمارهم عن 50 = (1 – 0.9772) × 400 = 0.0228 × 400 ≈ 9
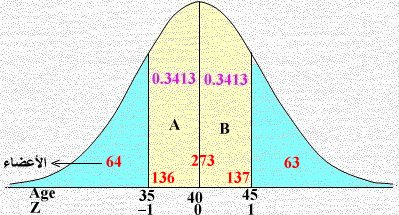
3) الأعضاء الذين أعمارهم أقل من 35 واكبر من 45 هم خارج الفترة العمرية للمطلوب 1)
والمبينة بالشكل المقابل باللون الأزرق وهي تمثل 1 مطروحاً منه المساحة 0.6826 أي:
المساحة = 1– 0.6826
= 0.3174
عدد الأعضاء = 0.3174 × 400
≈ 127
وتمثلهم المساحة المبينة باللون الأزرق ـ أنظر الشكل المقابل ـ
احسب قيمة العلامة الزائية للمئين 85
الحـل:
المئين 85 تمثله 0.85 من المساحة تحت منحى التوزيع الطبيعي
من جدول Z نبحث في عمود المساحة عن القيمة 0.8500 فنجد القيمة 0.8504 وهي أقرب إلى 0.8500 من 0.8485 يقابلها في عمود Z القيمة 1.04
لاحظ:
للحصول على Z من الجدول يجب معرفة قيمة النسبة (المساحة تحت المنحنى الطبيعي) سواء كان لجزء من المائة (المئين) أو لنسبة مئوية 15% مثلاً سواء كانت أكثر أو أقل أو يساوي وبالتالي نبحث في جدول Z عن الكسر العشري 0.15 مثلاً ومنها نعرف قيمة Z من الجدول مباشرة للمفهوم يساوي أو أقل من، ولكن حال ذكر أكبر من 15% أي على يمين العدد وجدول Z يعطي قيم المساحة على يسار العدد (أقل من) فنبحث عن 85% التي تمثل يسار Z أو أقل من 85% المقابلة إلى 100% – 15% = 85%
ما العلامة التائية للعلامة الزائية للعلامة 75 وكذلك احسب العلامة الزائية للعلامة التائية 800
الحـل:
العلاقة الرياضية التي تربط العلامتان الزائية والتائية هي:
T = 10Z + 50 → (1)
يمكن صياغتها بالصورة الآتية:
Z = (T – 50) ÷ 10 → (2)
بالتعويض في (1) عن 75
T = 10Z + 50 → (1)
= 10×75 + 50
= 800
نعوض في (2) عن 800
Z = (T – 50) ÷ 10 → (2)
= (800 – 50) ÷ 10
= 750 ÷10
= 75
لاحظ: في حالة إعطاء علامات زائية وتائية وطَلب ترتيبها فيجب تحويل الزائية إلى تائية أو العكس
2) هناك علامة معيارية أخرى تعرف بدرجة SATت(Scholastic Aptitude Test) بوسط حسابي i500 وانحراف معياري i100حيث:
SAT = 100Z + 500
متوسط بيانات مجتمع 85 وانحرافه المعياري 20 فما قيمة الدرجة التائية التي تقابل العلامة 140.
الحـل:
العلاقة الرياضة المطلوبة لحساب Z هي:
Z = (X – μ) ÷ σ
= (140 – 85) ÷ 20
= 55 ÷ 20
= 2.75
نحول العلامة Z إلى علامة تائية من العلاقة الرياضية:
T = 10Z + 50
= 10×2.75 + 50
= 77.5
لاحظ : في حالة عدم معرفة الانحراف المعياري والوسط نعتمد الوسيط والمدى لحساب Z من العلاقة الرياضية:
الدرجة المعيارية Z = (الدرجة الخام – الوسيط) ÷ المدى الربيعي
اختير طالب عشوائياً من مجتمع نسبة ذكاء أفراده تتبع توزيع طبيعي وبمتوسط حسابي 80 وانحراف معياري 10 فأوجد:
1) احتمال أن تقل نسبة ذكاء الطالب المختار عن 90
2) احتمال أن تزيد نسبة ذكاء الطالب المختار عن 105
3) احتمال أن تتراوح نسبة ذكائه بين 90 ، 105
4) وضح ذلك بيانياً (المساحة تحت منحنى التوزيع الطبيعي).
الحـل:
1) نحسب العلامة
المعيارية (Z ) التي تقابل القيمة 90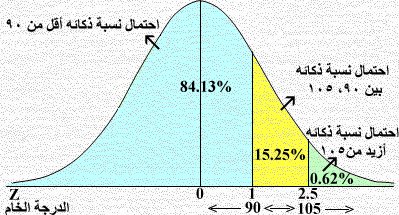
Z = (X – μ) ÷ σ
= (90 – 80) ÷ 10
= 1
من جدول Z نجد أن المساحة المقابلة = 0.8413 وهو الاحتمال المطلوب
2) نحسب العلامة المعيارية (Z ) التي تقابل القيمة 105
Z = (X – μ) ÷ σ
= (105 – 80) ÷ 10
= 2.5
من جدول Z نجد أن المساحة المقابلة = 0.9938
وحيث المطلوب أن تزيد نسبة الذكاء فيكون الاحتمال المطلوب = 1 – 0.9938 = 0.0062
3) الاحتمال المطلوب = احتمال أقل من 105 مطروحاً منه احتمال أقل من 90 أي:
P( 90 < X < 105 ) = P( X < 105 ) – P( X < 90 )
= P( Z < 2.5 ) – P( Z < 1 )
= 0.9938 – 0.8413
= 0.1525
4) مبين بالشكل، لاحظ مجموع الاحتمالات الثلاثة يساوي الواحد الصحيح.
رتب العلامات التالية ترتيباً تنازلياً:
علامة تائية i80 ، وعلامة زائية i3.2 ، ورتبة مئينية i70% ، وعلامة SATاi600
الحـل:
نحول العلامات إلى الزائية:
العلامة التائية 80 :
T = 10Z + 50
80 = 10Z + 50
Z = 3
الرتبة المئينية 70%:
من جدول Z أمام المساحة 0.7000 نجد:
Z = 0.85
علامة SATا4:
SAT = 100Z + 500
600 = 100Z + 500
Z = (600 – 500) ÷ 100
Z = 1
الترتيب:
i 0.85 , 1 , 3 , 3.2
برهن على أنَّ مجموع مربعات العلامات الزائية لقيم مفردات مجتمع يساوي عدد هذه المفردات (n) وللعينة عدد مفرداتها مطروحاً منه الواحد الصحيح (n–1).
الحـل:
مجموع مربعات علامات زائية لقيم مفردات مجتمعي يساوي عدد المفردات
بالنسبة للمجتمع يكون المجموع يساوي n وللعينة n –1 وهنا برهان ذلك للمجتمع وللعينة نكتفي باستبدال n بـ n –1
لتكن لدينا مجموعة من القيم:
Xi , i = 1, 2, 3, ..., n
وسطها الحسابي يحتسب من العلاقة الرياضية:
∑Xi
`X = ——
n
مجموع فروق القيم عن وسطها = صفر
∑(Xi –`X ) = 0
التباين S2 يحسب من العلاقة الرياضية التالية:
∑(Xi –`X )2
S2 = ————— → (1)
n
الانحراف المعياري σ يساوي الجذر ألتربيعي للتباين
نحسب قيمة العلامة الزائية من العلاقة الرياضية:
(Xi –`X )
Z = —————
S
نربع طرفي المعادلة السابقة فنحصل على:
(Xi –`X )2
Z2 = —————
S2
نجمع طرفي المعادلة:
∑(Xi –`X )2
∑Z2 = ——————
S2
نعوض عن قيمة S2 من (1)
∑(Xi –`X )2
∑Z2 = —————— × n
∑(Xi –`X )2
= n
فمثلاً : مجموع مربعات 6 علامات زائية هو 6 للمجتمع ، 5 للعينة
لاحظ أنَّ: مجموع العلامات الزائية لقيم مفردات مجتمع (أو عينة) يساوي صفر
جدول Z حيث النتائج التالية من التعويض (برنامج EXCEL) عن قيم Z في القانون التالي:
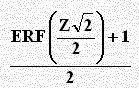
| Z | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
| 0.0 | 0.5000 | 0.5040 | 0.5080 | 0.5120 | 0.5160 | 0.5199 | 0.5239 | 0.5279 | 0.5319 | 0.5359 |
| 0.1 | 0.5398 | 0.5438 | 0.5478 | 0.5517 | 0.5557 | 0.5596 | 0.5636 | 0.5675 | 0.5714 | 0.5753 |
| 0.2 | 0.5793 | 0.5832 | 0.5871 | 0.5910 | 0.5948 | 0.5987 | 0.6026 | 0.6064 | 0.6103 | 0.6141 |
| 0.3 | 0.6179 | 0.6217 | 0.6255 | 0.6293 | 0.6331 | 0.6368 | 0.6406 | 0.6443 | 0.6480 | 0.6517 |
| 0.4 | 0.6554 | 0.6591 | 0.6628 | 0.6664 | 0.6700 | 0.6736 | 0.6772 | 0.6808 | 0.6844 | 0.6879 |
| 0.5 | 0.6915 | 0.6950 | 0.6985 | 0.7019 | 0.7054 | 0.7088 | 0.7123 | 0.7157 | 0.7190 | 0.7224 |
| 0.6 | 0.7257 | 0.7291 | 0.7324 | 0.7357 | 0.7389 | 0.7422 | 0.7454 | 0.7486 | 0.7517 | 0.7549 |
| 0.7 | 0.7580 | 0.7611 | 0.7642 | 0.7673 | 0.7704 | 0.7734 | 0.7764 | 0.7794 | 0.7823 | 0.7852 |
| 0.8 | 0.7881 | 0.7910 | 0.7939 | 0.7967 | 0.7995 | 0.8023 | 0.8051 | 0.8078 | 0.8106 | 0.8133 |
| 0.9 | 0.8159 | 0.8186 | 0.8212 | 0.8238 | 0.8264 | 0.8289 | 0.8315 | 0.8340 | 0.8365 | 0.8389 |
| 1.0 | 0.8413 | 0.8438 | 0.8461 | 0.8485 | 0.8508 | 0.8531 | 0.8554 | 0.8577 | 0.8599 | 0.8621 |
| 1.1 | 0.8643 | 0.8665 | 0.8686 | 0.8708 | 0.8729 | 0.8749 | 0.8770 | 0.8790 | 0.8810 | 0.8830 |
| 1.2 | 0.8849 | 0.8869 | 0.8888 | 0.8907 | 0.8925 | 0.8944 | 0.8962 | 0.8980 | 0.8997 | 0.9015 |
| 1.3 | 0.9032 | 0.9049 | 0.9066 | 0.9082 | 0.9099 | 0.9115 | 0.9131 | 0.9147 | 0.9162 | 0.9177 |
| 1.4 | 0.9192 | 0.9207 | 0.9222 | 0.9236 | 0.9251 | 0.9265 | 0.9279 | 0.9292 | 0.9306 | 0.9319 |
| 1.5 | 0.9332 | 0.9345 | 0.9357 | 0.9370 | 0.9382 | 0.9394 | 0.9406 | 0.9418 | 0.9429 | 0.9441 |
| 1.6 | 0.9452 | 0.9463 | 0.9474 | 0.9484 | 0.9495 | 0.9505 | 0.9515 | 0.9525 | 0.9535 | 0.9545 |
| 1.7 | 0.9554 | 0.9564 | 0.9573 | 0.9582 | 0.9591 | 0.9599 | 0.9608 | 0.9616 | 0.9625 | 0.9633 |
| 1.8 | 0.9641 | 0.9649 | 0.9656 | 0.9664 | 0.9671 | 0.9678 | 0.9686 | 0.9693 | 0.9699 | 0.9706 |
| 1.9 | 0.9713 | 0.9719 | 0.9726 | 0.9732 | 0.9738 | 0.9744 | 0.9750 | 0.9756 | 0.9761 | 0.9767 |
| 2.0 | 0.9772 | 0.9778 | 0.9783 | 0.9788 | 0.9793 | 0.9798 | 0.9803 | 0.9808 | 0.9812 | 0.9817 |
| 2.1 | 0.9821 | 0.9826 | 0.9830 | 0.9834 | 0.9838 | 0.9842 | 0.9846 | 0.9850 | 0.9854 | 0.9857 |
| 2.2 | 0.9861 | 0.9864 | 0.9868 | 0.9871 | 0.9875 | 0.9878 | 0.9881 | 0.9884 | 0.9887 | 0.9890 |
| 2.3 | 0.9893 | 0.9896 | 0.9898 | 0.9901 | 0.9904 | 0.9906 | 0.9909 | 0.9911 | 0.9913 | 0.9916 |
| 2.4 | 0.9918 | 0.9920 | 0.9922 | 0.9925 | 0.9927 | 0.9929 | 0.9931 | 0.9932 | 0.9934 | 0.9936 |
| 2.5 | 0.9938 | 0.9940 | 0.9941 | 0.9943 | 0.9945 | 0.9946 | 0.9948 | 0.9949 | 0.9951 | 0.9952 |
| 2.6 | 0.9953 | 0.9955 | 0.9956 | 0.9957 | 0.9959 | 0.9960 | 0.9961 | 0.9962 | 0.9963 | 0.9964 |
| 2.7 | 0.9965 | 0.9966 | 0.9967 | 0.9968 | 0.9969 | 0.9970 | 0.9971 | 0.9972 | 0.9973 | 0.9974 |
| 2.8 | 0.9974 | 0.9975 | 0.9976 | 0.9977 | 0.9977 | 0.9978 | 0.9979 | 0.9979 | 0.9980 | 0.9981 |
| 2.9 | 0.9981 | 0.9982 | 0.9982 | 0.9983 | 0.9984 | 0.9984 | 0.9985 | 0.9985 | 0.9986 | 0.9986 |
| 3.0 | 0.9987 | 0.9987 | 0.9987 | 0.9988 | 0.9988 | 0.9989 | 0.9989 | 0.9989 | 0.9990 | 0.9990 |