الدرجات المعيارية Standard Scores

    ذكرنا سابقاً ودون تفصيل عن الدرجة المعيارية والتي رمزنا لها بالرمز Z وهنا نستعرض بالتفصيل الدرجة المعيارية.

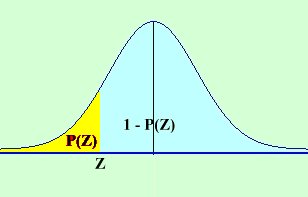
عرفنا التوزيع الطبيعي المعياري بأنه التوزيع الطبيعي الذي وسطه صفراً وانحرافه المعياري الواحد الصحيح ويرمز لمتغيره العشوائي بالرمز Z حيث قيم Z هي قيمة المساحة الواقعة على يسار Z فوق المحور الأفقي وتحت المنحنى كما مبين بالشكل المقابل باللون الأصفر حيث P(Z)s المساحة وهي قيمة احتمال Z أيضاَ والمساحة تحت المنحنى تساوي الواحد الصحيح وقد تكون قيمة Z موجبة أو سالبة وإن Z = 0 تقع في المنتصف أي تقسم المساحة لقسمين متساويين كل منهم يساوي 0.5

    إذا لم يكن الوسط الحسابي صفراً والانحراف المعياري الواحد الصحيح فالمتغير الطبيعي هنا غير معياري وسطه μ ، الانحراف المعياري σ فإن:

 Z = (x – μ)÷σ   للمجتمع أو

 Z = ( x –`X ) ÷ s   للعينة                                                                             حساب Z,T باستخدام SPSS

حيث s الانحراف المعياري أو

x = Z s +`X  وهذه معادلة خطية وعليه يكون التحويل خطي

تعريف: الدرجة المعيارية هي تعبير كمي عن درجة المشاهدة لتحديد موقعها النسبي في العينة أو المجتمع.     مثال

من حيث الدرجة الخام (المشاهدة) لا تعكس واقع صاحبها بصرف النظر عن قيمتها فدرجة طالب في مادة ما 90 لا تعني أنه طالب ممتاز حال جميع أفراد مجموعته حصلوا على درجة أكبر من 90 والعكس فلا تعني حصوله على الدرجة 65 بأنه متوسط المستوى إذا عرف بأن جميع أفراد مجموعته حصلوا على درجة أقل من 65 فالدرجة المعيارية المقابلة للدرجة الخام (Z) تأخذ في الاعتبار النزعة المركزية (الوسط الحسابي) والتشتت (الانحراف المعياري) لكافة أفراد المجموعة، وتكون الدرجة المعيارية موجبة إذا كانت أكبر من الوسط الحسابي وصفراً حال مساواتها بالوسط الحسابي وسالبة إذا كانت أقل من الوسط الحسابي، وعلى العموم تكون مساوية للفرق بينها وبين مركز التوزيع مقسوماً على تشتتا لتوزيع.

    والشكل الآتي يبين المساحة تحت المنحى للعلامة المعيارية (Z) بمقدار انحرافات معيارية حسب كون Z تساوي ...، –1، 0، 1، ...

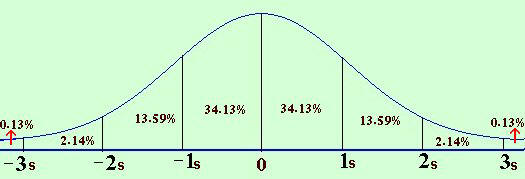
    والجدول هنا يبن قيم المساحة أو الاحتمال المقابلة لقيم Z وبالعكس.