إيجاد حجم جسم باستخدام التكامل
الجسم الدوراني هو الناشئ من دوران شكل هندسي مستو حول مستقيم واقع في مستوى الشكل الهندسي فمثلاً:
ينشأ المخروط الدائري القائم من دوران مثلث قائم حول أحد ضلعي القائمة، الضلع هو محور الدوران
تنشأ الأسطوانة الدارئة القائمة من دوران مستطيل حول أحد أضلاعه، الضلع هو محور الدوران
تنشأ الكرة من دوران نصف دائرة حول قطرها، القطر هو محور الدوران
ويجب ملاحظة أن مقطع الجسم الدوراني بمستو عمودي على محور الدوران هو دائرة. وسنذكر هنا محور الدوران أما أن يكون محور السينات أو محور الصادات.
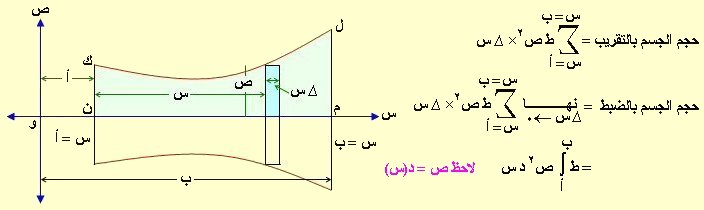
ليكن لدينا المنحنى ص = د(س) والمطلوب إيجاد حجم الجسم الناشئ من دوران المساحة المحدود بمنحنى الدالة والمستقيمان س = أ ، س = ب حول محور السينات، لذا نقسم المساحة إلى مستطيلات صغيرة (المستطيل الأزرق) فيكون الحجم هو نهاية مجموع الاسطوانات الناشئة عن دوران هذه المستطيلات وبأخذ ص طولاً لمستطيل ، ∆ س عرضاً له ويكون حجم الاسطوانة الناشئة = ط ص2× ∆ س (لاحظ الشكل).

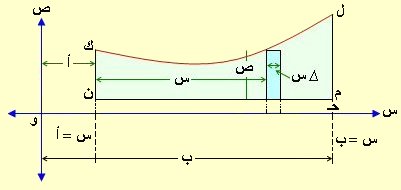
نتيجة1: إذا دارت المساحة ل م ن ك حول محور السينات ، م ن
يوازي محور السينات وعلى بعد حـ منه فإن الحجــم الجزئــــي
عبارة عن اسطوانة جوفاء = ط ص2× ∆ س – ط حـ2× ∆ س
= ط(ص2– حـ2) ∆ س
فالحجم يساوي نهاية المجموع من أ إلى ب عندما ∆ س ←0 أي:
ب
ح = ط ∫ (ص2 – حـ2) د س
أ
نتيجة2: إذا دارت المساحة ل م ن ك حول في الشكل السابق حول المستقيم م ن فإن الحجم الجزئي عبارة عن اسطوانة نصف قطرها ( ص – حـ ) وارتفاعها ∆ س وحجمها = ط (ص – حـ)2 × ∆ س
ويكون الحجم للجسم الناشئ يساوي نهاية المجموع من أ إلى ب عندما ∆ س ←0 أي:
ب 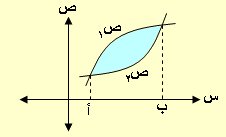
ح = ط ∫ (ص – حـ)2 د س
أ
نتيجة 3: حجم الجسم الناشئ من دوران المنطقة المحصورة بين منحنيي الدالتين ص1 ، ص2
دورة كاملة حول محور السينات كما مبين بالشكل هو:
ب
ح = ط ∫ [(ص1)2 – (ص2)2] د س أ ، ب الاحداثيان السينيان لنقطتي تقاطع المنحنيين
أ
حجم المخروط القائم ، القائم الناقص
إيجاد حجم المنطقة الكروية والقطعة الكروية ونصف الكرة والكرة