إيجاد حجم المنطقة الكروية والقطعة الكروية ونصف الكرة والكرة
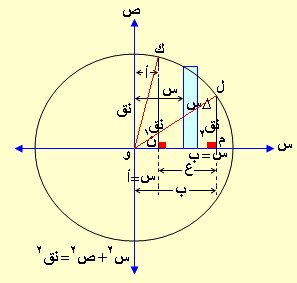
لنأخذ دائرة نصف قطرها نق ومركزها نقطة الأصل س2+ ص2= نق2
تنشأ المنطقة الكروية من دوران المساحة ل م ن ك، والمحددة بالقوس ل ك من منحنى الدائرة ومحور السينات والمستقيمان س = أ ، س = ب حول محور السينات ويكون الحجم الجزئي يساوي ط ص2 × ∆ س والحجم الكلي هو نهاية مجموع الحجم الجزئي من أ إلى ب عندما ∆ س ←0 أي أن:
ب
ح = ط ∫ ص2 د س
أ
ب
= ط ∫ ( نق2– س2) د س
أ
ب
س3 ب2 أ3
= ط [ نق2س – ـــــــ ] = ط [( نق2ب – ــــــ ) – ( نق2 أ – ــــــ ) ]
3 3 3
أ
1
= ط [نق2( ب – أ ) – ــــ ( ب3 – أ3 )] أي أن:
3
ط( ب – أ)
حجم المنطقة الكروية = ــــــــــــــــــــ [3 نق2 – ( ب2+ أ ب + أ2)] ← (1)
3
بحذف أ ، ب يمكن وضع القانون (1) بدلالة نصفي قطري قاعدة المنطقة نق1 ، نق2 ، ارتفاعها ع كما يلي:
ط ع
حجم المنطقة الكروية = ـــــــــ[6 نق2 – 2( ب2+ أ ب + أ2)] لاحظ ضربنا × 2 وقسمنا ÷ 2
6
ط ع
حجم المنطقة الكروية = ـــــــــ[3 نق2 + 3 نق2– 2( ب2+ أ ب + أ2)] 6 نق2 =3 نق2 + 3 نق2
6
ط ع
حجم المنطقة الكروية = ـــــــــ[3( (نق1)2 + أ2) + 3 ( (نق2)2 + ب2) – 2( ب2+ أ ب + أ2)] بالتعويض عن نق2
6
ط ع
حجم المنطقة الكروية = ـــــــــ[3( (نق1)2 + (نق2)2) + ( ب2–2أ ب + أ2)]
6
ط ع
حجم المنطقة الكروية = ـــــــــ[3( (نق1)2 + (نق2)2) + ( ب – أ)2]
6
ط ع
حجم المنطقة الكروية = ـــــــــ[3 ( نق2+ نق2) + ع2] ← (2)
6 1 2
بوضع نق2 = 0 فالمنطقة الكروية تصبح قطعة كروية نصف قطر قاعدتها نق1 وارتفاعها ع وبالتعويض في (2) يكون:
ط ع
حجم القطعة الكروية = ـــــــــ[3 نق2 + ع2] ← (3)
6 1
وبوضع نق2 = 0 ، نق1 = نق فإن ع تؤول إلى نق والمنطقة الكروية تؤول إلى نصف كرة قطرها نق وبالتعويض في (2)
ط نق
حجم نصف الكرة = ــــــــــ[3 ( نق2+ 0) + نق2]
6
2
حجم نصف الكرة = ـــــ ط نق3 ← (4)
3
وبوضع نق2 = 0 ، نق1 = 0 ، ع = نق فالمنطقة الكروية تؤول إلى كرة وبالتعويض في (2) فإن:
ط × 2 نق
حجم المنطقة الكروية = ـــــــــــــــــــ[3 (0 + 0 ) + (2نق)2]
6
ط × 2 نق
حجم المنطقة الكروية = ـــــــــــــــــــ[4 نق2]
6
4
 حجم المنطقة الكروية = ــــــ ط نق3 ← (5)
لاحظ : يمكن التوصل للقوانين السابقة عن طريق التكامل بالتعويض
حجم المنطقة الكروية = ــــــ ط نق3 ← (5)
لاحظ : يمكن التوصل للقوانين السابقة عن طريق التكامل بالتعويض
3