سوف يتبع نفس الأسلوب السابق عند حساب المساحة في تحديد الفترة فأما أن تعطى مباشرة أو تحسب بوضع ص = 0 إذا كان محور الدوران هو المحور السيني والحال نفسه إذا كان محور الدوران هو محور الصادات والبرهان بنفس الطريقة (محور السينات) والقانون مبين في السطر التالي

                                ب                                                                             ب

ويكون القانون :  ح = ط ∫  ص² د س   للدوران حول محور السينات  والقانون ح = ط ∫  س² د ص للدوران حول محور الصادات

                                 أ                                                                              أ

                                                                                                                      ـــــــــــــــــ

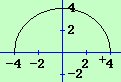
مثال (1): أوجد حجم الجسم الناشئ من دوران المنطقة المحصورة بين محنى الدالة ص = /\16– س²  ومحور السينات دورة كاملة حول محور

             السينات

الحــل : بوضع ص = 0 لأن الفترة لم تذكر هنا والدوران حول المحور السيني

           16– س² = صفر

            س = ± 4 فالفترة هي [ –4 ، 4 ] أي أن:

                       ب                      4                                 4                                                             4

            ح = ط ∫  ص² د س  = ط ∫  ( 16– س²) د س = 2ط ∫ ( 16– س²) د س = 2ط [ 16س – (س³÷ 3) ]

                     أ                       –4                                 0                                                              0 

                                          64                16×4×3 – 64                128      256

                = 2ط [ 16 × 4 – ـــــــ ] = 2ط ( ــــــــــــــــــــــــــــــــ ) = 2ط × ــــــــــ = ــــــــــــ ط

                                           3                           3                            3          3 

لاحظ : الجسم الناشئ عن الدوران هو كرة نصف قطرها 4

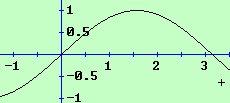
مثال (2): أوجد حجم الجسم الناشئ من دوران المنطقة المحصورة بين محنى الدالة ص = حاس ومحور السينات في الفترة [ 0 ، ط ] دورة كاملة حول

              محور السينات

الحــل : 

                       ب                      ط 

            ح = ط ∫  ص² د س  = ط ∫  حا²س  د س

                     أ                         0 

                                      1

            ومن حيث حا²س = ــــ ( 1 – حتا2س ) وبإجراء التكامل بالنسبة إلى س يكون:

                                      2 

                         1            حا2س     ط

            ح = ط [ ــــ( س – ــــــــــــــ ) ]   وبإجراء التكامل بالنسبة إلى س يكون:

                         2               2       0

                         1           حا2ط                   ط² 

            ح = ط× ــــ( ط – ــــــــــــــ ) – صفر = ـــــ

                        2             2                       2

مثال (3): أوجد حجم الجسم الناشئ من دوران المنطقة المحددة بالمحنيين ص = 3 س² ، ص = 3 س إذا دارت المنطقة دورة كاملة حول محور

              السينات ( وضح بالرسم إن أمكن ).

الحــل :  بمساواة الطرف الأيسر للمنحنيين

            3 س²= 3 س   أي   3س( س – 1 ) = 0  ومنها  س = 0 ، س = 1  حدا التكامل

برسم المنحنيات أو بوضع س = 0.5 ' [ 0 ، 1 ] فتكون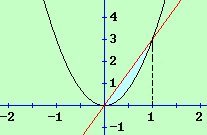

ص₁ = 3 × 0.25 = 0.75 ، ص₂ = 3 × 0.5 = 1.5 أي أن  ص₂ > ص₁ عند س = 0.5

                       ب  

            ح = ط ∫  [(ص₂)² – (ص₁)²] د س  ، ص₂ = 3 س منحنى يمثله خط مستقيم (الأحمر)

                     أ                                          ص₁ = 3س² ممثل بمنحنى القطع المكافئ            

                      1                                                       

            ح = ط ∫  [(3س)² – (3س²)²] د س    من التعويض عن ص₂ ، ص₁

                     0

                       1

            ح = ط ∫  [9س² – 9س⁴] د س           بإجراء عملية التكامل نحصل على

                     0

                            س³     س⁵  1

            ح = 9 ط [ ـــــــ  – ـــــــ ]                    بالتعويض عن س = 1 ، س = 0 ( التعويض عن الصفر يعطي القيمة صفر)

                            3        5    0

                            1      1

            ح = 9 ط [ ــــ  – ـــــ ]                   بأخذ 15 كمقام مشترك والاختصار نحصل على الحجم المطلوب

                            3      5     

            ح = 1.2 ط