الانحدار غير الخطي المتعدد Non-Linear Multiple Regression

    سبق أن ذكرنا في مقدمة الانحدار غير الخطي البسيط بوجود أنواع من الانحدار غير الخطي والتي تضم العنصر X2 أو X3 أي إضافة أحد العنصرين  X2 أو X3 لمعادلة الانحدار غير الخطي البسيط ونحصل على معادلة الانحدار ألتربيعي ، ومعادلة الانحدار التكعيبي وسيتم عرضها هنا.

معادلة الانحدار ألتربيعي Quadratic Regression Equations                    معادلة الانحدار التكعيبي Cubic Regression Equation

    هذه المعادلة تعتبر من أبسط معادلات الانحدار غير الخطي المتعدد وهي معادلة من الدرجة الثانية ونشأت من إضافة العنصر X2  لمعادلة الانحدار الخطي البسيط وتأخذ الصورة الآتية:

 y = a + b X + c X2

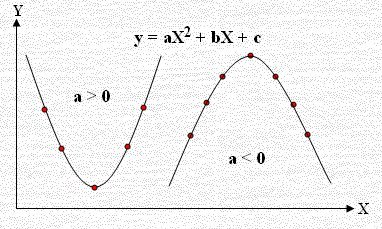
 والمنحنى قطع مكافئ مفتوح من أعلى  (معامل  X2 موجب a > 0) ورأسه نقطة صغرى أو مفتوح من أسف  (معامل  X2 سالب a < 0) ورأسه نقطة عظمى والرأس في الحالتين له إحداثي سيني = – (b ÷ 2a) لاحظ الشكل:

لتحويل معادلة الانحدار ألتربيعي لمعادلة خطية نفرض الآتي:

   X1 = X    ,    X2 = X2  فتكون لدينا الصيغة:

y = a + b X1+ c X2  وبالتالي يمكن إيجاد قيم الثوابت باستخدام طريقة المربعات الصغرى وبنفس الطريقة التي استخدمت في معادلة الانحدار الخطي المتعدد  لحل المعادلات الثلاث التالية وسنفصل ذلك بالمثال التالي:

 ∑Y = na + b∑X1 + c ∑X2

 ∑X1Y = a∑X1 + b∑X12 + c ∑X1X2

 ∑X2Y = a∑X2 + b∑X1X2 + c ∑X22

مثال:

    أوجد معادلة الانحدار ألتربيعي من جدول التوزيع التالي والذي يبين عدد الوحدات المنتجة بالمئات لستة أنواع من أجهزة الراديو (X) ومعدل كلفة الجهاز الواحد المنتج بالدينار البحريني (Y) ثم أوجد تقدير كلفة الجهاز الواحد عند X = 3.5 وأرسم الخط البياني للمعادلة.

6 5 4 3 2 1 عدد الأجهزة (X)
6 4 5 4 2 3 تكلفة الوحدة (Y)

الحل:

    نكون جدول البيانات المطلوبة لحل المعادلات الثلاث أعلاه للتعرف على قيم الثوابت a , b , c

Y2 X22 X12 X1X2 X2Y X1Y

X2 (X2)

 Y X (X1)
9 1 1 1 3 3 1 3 1
4 16 4 8 8 4 4 2 2
16 81 9 27 36 12 9 4 3
25 256 16 64 80 20 16 5 4
16 625 25 125 100 20 25 4 5
36 1296 36 216 216 36 36 6 6
106 2275 91 441 433 95 91 24

Total 21

المعادلات المطلوب حلها هي:

24 = 6a + 21b +91c

95 = 21a + 91b + 441c

433 = 91a + 441b + 2275c

طرق حساب الثوابت

ناتج حل المعادلات

 المعادلات بعد التعويض من الجدول أعلاه(الصف الأخير)

 المعادلات

 a = 2.3

  b = 0.254  

 c = 0.054

24 = 6a + 21b +91c

95= 21a + 91b + 441c

433 = 91a + 441b + 2275c

 ∑Y = na + b∑X1 + c ∑X2

 ∑X1Y = a∑X1 + b∑X12 + c ∑X1X2

 ∑X2Y = a∑X2 + b∑X1X2 + c ∑X22

معادلة الانحدار ألتربيعي هي:  Y = 2.3 + 0.254 X1 + 0.054 X2  أي Y = 0.054 X2 + 0.254 X + 2.3

معدل كلفة الجهاز الواحد عند X = 3.5 ، نعوض في المعادلة لحساب Y أي:

Y = 0.054(3.5)2 + 0.254(3.5) + 2.3

Y = 0.6615 + 0.889 + 2.3

Y = 3.8505 ≈ 3.9

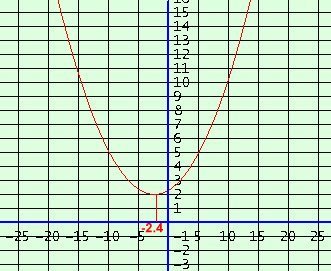
التمثيل البياني: ألإحداثي السيني لرأس القطع المكافئ = – 0.254 ÷ 2× 0.054 = – 0.254 ÷ 0.108 = – 2.4

                    ألإحداثي الصادي لرأس القطع المكافئ =  0.054( –2.4 )2 + 0.0254( –2.4 ) + 2.3 = 2

                    رأس القطع المكافئ ( – 2.4 ، 2) وهو مفتوح من أعلى كما مبين بالشكل