والتمثيل
البياني للمعادلة التكعيبية يبينها الشكل التالي حيث أن:الانحدار غير الخطي المتعدد Non-Linear Multiple Regression
معادلة الانحدار التكعيبي Cubic Regression Equation
هذه المعادلة من الدرجة الثالثة وهي امتداد للمعادلة التربيعية والحاجة للقوة الثالثة أي الدرجة الثالثة أي إضافة X3 للمعادلة التربيعية لتضبيط البيانات الموجودة والصورة العامة لمعادلة الدرجة الثالثة (التكعيبية) هي:
Y = a + bX + cX2 + dX3
نحول هذه المعادلة لصورة خطية بفرض: X = X1 , X2 = X2 , X3 = X3 فتكون المعادلة الخطية بعد الفرضية هذه هي:
Y = a + bX1 + cX2 + dX3
ويمكن حساب قيم الثوابت هنا a , b , c , d جبريا وهو أمر ليس بالسهل ولذا نستخدم الحاسب الآلي من خلال SPSS , MINITAB , ...
والتمثيل
البياني للمعادلة التكعيبية يبينها الشكل التالي حيث أن:
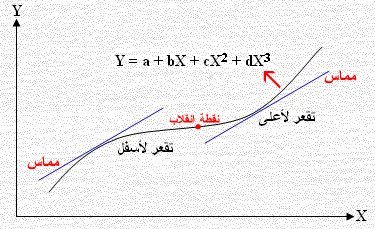
التقعر لأعلى: المنحنى يقع فوق مماساته.
التقعر لأسفل: المنحنى يقع أسفل مماساته.
قطة الانقلاب: النقطة التي يتحول عندها المنحنى من تقعره لأسفل إلى تقعره لأعلى
أو هي النقطة التي تكون عندها المشتقة الثانية تساوي صفر.
والشكل يبين شكل المعادلة Y = a + bX + cX2 + dX3 وهو الصورة العامة لمعادلة الدرجة الثالثة.
مثال:
مستعيناً ببرنامج MINITAB أوجد معادلة الانحدار التكعيبي من جدول التوزيع التالي والذي يبين عدد الوحدات المنتجة بالمئات لستة أنواع من أجهزة الراديو (X) ومعدل كلفة الجهاز الواحد المنتج بالدينار البحريني (Y) وأرسم الخط البياني للمعادلة.
| 6 | 5 | 4 | 3 | 2 | 1 | عدد الأجهزة (X) |
| 6 | 4 | 5 | 4 | 2 | 3 | تكلفة الوحدة (Y) |
الحل:
نتبع نفس الطريقة التي استخدمت في المثال السابق لمعرفة المعادلة التربيعية باستخدام برنامج MINITAB مع إضافة المتغير الجديد X3 للمتغيرين X1 , X2 وبالتالي نحصل على المعادلة وقيم الثوابت وهي: 3 ، 0.63 ، 0.35 ، 0.028 لقيم a , b , c , d والمعادلة الخطية من صفحة نتائج MINITAB وهي:
The regression equation is
Y = 3.00 – 0.63 x1 + 0.35 x2 – 0.028 X3
Predictor Coef SE Coef T P
Constant 3.000 4.363 0.69 0.563
x1 – 0.627 4.971 – 0.13 0.911
x2 0.345 1.591 0.22 0.848
X3 – 0.0278 0.1503 – 0.18 0.870
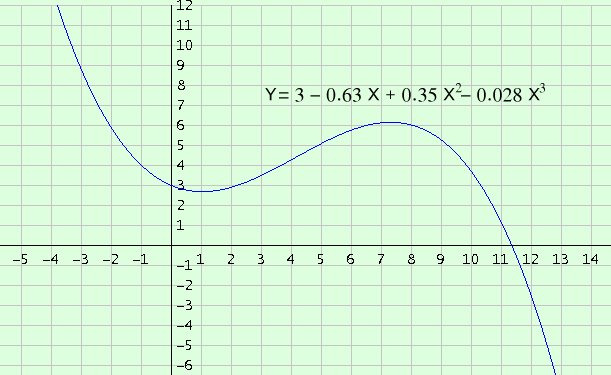
والمعادلة التكعيبية بعد إعادة الفرضية للمتغير X الأصل هي: Y = 3 – 0.63X + 0.35 x2 – 0.028 X3
والتمثيل البياني لها مبين بالشكل الآتي:
