ملاحظة عن المشتقة الأولى للدالة
المشتقة الأولى للدالة Y = aXn +bXn-1 + ... + c بالنسبة للمتغير X هي Y\ = a(n)Xn–1 + b(n–1)Xn–2 + ....c تكون أصغر قيمة ممكنة للمتغير التابع Y عندما تكون المشتقة الأولى تساوي الصفر أو عند X المتغير المستقل الذي يجعل المشتقة الأولى يساوي الصفر ويهمنا هنا مشتقة مقار مربع بالصورة ( أ + ب س)2 بالنسبة للمتغير س حيث تكون المشتقة الأولى أس القوس × القوس للأس السابق مطروحاً منه واحد صحيح × مشتقة ما بداخل القوس أي مشتقة القوس هنا هي 2(أ + ب س) × ب وللمعلومات ذات تفاصيل أكثر في هذا المجال راجع العنوان:D:\ehsa\analysisa/derived.htm

برهان المعادلة الاعتدالية لخط المربعات الصغرى
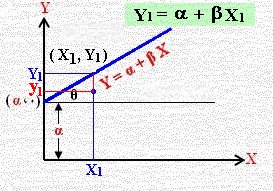
بفرض المعادلة المطلوبة هي Y = a + b X حيث β ميل الخط المستقيم ، α الجزء الذي يقطعه المستقيم من المحور الرأسي (الصادات) كما بينا ذلك سابقاً والموضح هنا في الشكل.
إن قيم Y = y1 + y2 + y3 + ... + yn الواقعة على الخط مقابلة لقيم X = X1 + X2 + X3 + ... + Xn في حين القيم الفعلية للمتغير التابع Y هي y1 , y2 , y3 , ... , yn والمسافة الرأسية (الانحراف عن الخط) والمبينة في الشكل Y1 – y1 = a + b X1 – y1
وبفرض S مجموع المربعات للانحرافات الناتجة، فللحصول على أصغر قيمة ممكنة للكمية S ( نهاية صغرى ) عندما تكون التفاضلات الجزئية لها بالنسبة إلى a , b تساوي الصفر (شرط النهاية الصغرى) وبالاشتقاق ووضع المشتقة تساوي الصفر وإجراء العمليات الجبرية على الناتج نحصل على:
ٍS = (a + b X1 – y1)2 + (a + b X2 – y2)2 + (a + b X3 – y3)2 + ... + (a + b Xn – yn)2
əS
— = 2(a + b X1 – y1) + 2(a + b X2 – y2) + 2(a + b X3 – y3) + ... + 2(a + b Xn – yn) = 0
əa
2(a + b X1 – y1) + 2(a + b X2 – y2) + 2(a + b X3 – y3) + ... + 2(a + b Xn – yn) = 0
(a + b X1 – y1) + (a + b X2 – y2) + (a + b X3 – y3) + ... + (a + b Xn – yn) = 0
na + b(X1 + X2 + X3 + ... + Xn) – (y1 + y2 + y3 + ... + yn) = 0
na + b ∑X – ∑Y = 0
∑Y = na + b ∑X ....... (1)
əS
— = 2(a + b X1 – y1)X1 + 2(a + b X2 – y2)X2 + 2(a + b X3 – y3)X3 + ... + 2(a + b Xn – yn)Xn = 0
əb
2(a + b X1 – y1)X1 + 2(a + b X2 – y2)X2 + 2(a + b X3 – y3)X3 + ... + 2(a + b Xn – yn)Xn = 0
(aX1 + b X12 – y1X1) + (aX1 + b X22 – y2X2) + (aX3 + b X32 – y3X3) + ... + (aXn + b Xn2 – ynXn) = 0
(aX1 + aX1 + aX3 +... +aXn ) + (b X12 + b X22 + b X32 ... + b Xn2) – (y1X1 + y2X2 + y3X3 + ... + ynXn ) = 0
a(X1 + X1 + X3 +... + Xn ) + b(X12 + X22 + X32 ... + Xn2) – (y1X1 + y2X2 + y3X3 + ... + ynXn ) = 0
a∑X + b ∑X2 – ∑(XY) = 0
∑(XY) = a ∑X + b ∑X2 ....... (2)
ـــــــــــ أوـــــــــ
المعادلة Y = a + b X إذا قمنا بعملية التجمع إلى n مرة نحصل على مجموع Y هو Y∑ وبالمثل مجموع a هو na ومجموع bX هو b ∑ X فنحصل على المعادلة:
ـ∑Y = na + b ∑X
وإذا ضربنا Y = a + b X في X نحصل على XY = aX + b X2 ولنجمع كما سبق أعلاه فنحصل على المعادلة الثانية:
∑(XY) = a ∑X + b ∑X2
ـــــــــــ أوـــــــــ
