
عدم التحيز ( Unbiasedness ) الكفاءة ( Efficiency ) التوافق أو الاتساق ( Consistency ) راجع التقدير بفترة
الإحصاء الاستدلالي أو التحليلي:
الهدف من الإحصاء الاستدلالي استنتاج خصائص المجتمع من خصائص عينة سحبت منه, فعند استخدام بيانات العينة (Statistic) للاستدلال عن المجتمع ولكوننا لا نملك كل حقائق المجتمع فنحث عن طريقة عملية نستطيع من خلالها الوثوق بالحقيقة المطلوبة ضمن نطاق معين معتمدين على طبيعة المجتمع المطلوب تقدير معاملاته( Parameter ) محاولين الوصول لقيم (العددية) لمعالم المجتمع من خلال بيانات العينة المسحوبة منه عشوائياً.
وينقسم الاستدلال الإحصائي لقسمين ، الأول التقدير الإحصائي (statistical estimation) والثاني اختبارات الفروض الإحصائية (hypothesis testing) فالأول يشير للطرق المختلفة لتقدير معالم المجتمع المجهولة في حين يشير الثاني إلى اختيرا بين أقوال حول قيم معالم المجتمع وكلاهما يستدل على معالم المجتمع المجهولة بالنسبة للسؤال محل البحث ومن الممكن استخدام كلاهما معاً حال تحليل البيانات، وينقسم الأول إلى تقدير بنقطة ( Point estimation) وتقدير بفترة ( Interval estimation) سيتم توضيح كل منهم لاحقاً.
المجتمع والعينة: Population and Sample
يعتبر اختبار الفروض أحد المواضيع الرئيسة للاستدلال الإحصائي ويهدف الوصول لخصائص المجتمع من خلال عينة منه قد سحبت بطريقة عشوائية حيث تعرف خصائص العينة بالإحصاءات، والإحصاءة ( Statistic ) قيمة رقمية تصف خاصية تعود للعينة في حين تعرف خصائص المجتمع بالمعالم، والمعلمة ( Parameter ) قيمة رقمية تصف خاصية تعود للمجتمع الإحصائي يستلزم قبولها أو رفضها حسب معطيات العينة المسحوبة وإن طرق الاستدلال تصنف حسب الهدف منه أما بالتقدير أو اختبار الفرض وهو ما يستلزم درجة الاعتمادية أو الثقة بنتائج العينة.
إن أساليب التقدير Estimation تهدف الوصول لبعض خواص المجتمع مثل تقدير خط الفقر أو نسبة الموافقين على مشروع ما أو تقدير متوسط دخل الأسرة على أن يكون التقدير غير متحيز ( تساوي الوسطين الحسابين للعينة والمجتمع ) وذو كفاءة والتوافق أو التناسق باقتراب قيمة التقدير إلى قيمة المعلمة وخاصة كلما زاد حجم المجتمع، والتقدير لمعالم المجتمع أما أن يكون تقدير بنقطة أو بفترة.
– N
إن التقدير غير المتحيز وكفؤاً في نفس الوقت كمتوسط العينة x وتباين العينة المعدل s2 ــــــــــــــــ = ŝ2 مثلان لذلك التقدير كما
(N–1)
إن التقدير غير المتحيز وغير كفؤا في نفس الوقت كوسيط العينة وإحصائية العينة ( Q1 + Q3) ½ مثلان لذلك التقدير، في حين التقدير المتحيز وغير كفؤاً في نفس الوقت كالانحراف المعياري s والانحراف المعياري المعدل ŝ والانحراف المتوسط ونصف المدى الربيعي أمثلة على ذلك.
التقدير بنقطة Point Estimation راجع التقدير بفترة
إذا قدرنا معلمة المجتمع بقيمة عددية واحدة فنعرف هذا بتقدير المعلمة بنقطة مثل قيمة الوسط الحسابي أو الانحراف المعياري باعتبارهم تقديراً لمعلمة المجتمع واهم طرق الحصول على التقدير هو مقدر الإمكان الأكبر ويتمتع بما ذكرناه كما أن تباين العينة S2 أو انحرافها المعياري تعرفنا بتقدير تباين المجتمع σ2، حيث معلمة التباين من العينة عبارة عن تباين العينة أي:

أهم التقديرات العادية للنقطة:
─ Σ x ¯ ^
1) تقدير الوسط الحسابي للمجتمع الغير معلوم حيث وسط العينة X = ــــــــــ فإن X هو تقدير μ أو مساوٍ له.
n
2) تقدير نسبة المجتمع إذا كانت غير معلومة فإن نسبة العينة p هي أفضل تقدير للنسبة في المجتمع π والخطأ المعياري هو
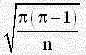
3) الانحراف المعياري للعينة أفضل تقدير مناسب للانحراف المعياري للمجتمع غير معلوم انحرافه المعياري.
4) تباين العينة S2 أفضل تقدير لتباين المجتمع σ2
ـــ
مثلاً إذا أردنا تقدير متوسط مجتمع وزن الدجاج في مزرعة وكان الوسط الحسابي (X) للعينة المسحوبة عشوائيا والمكونة من
ـــ
25 دجاجة يساوي 20 فإن X مقدر نقطة لمتوسط المجتمع μ في حين تعتبر القيمة 20 تقدير لهذا المتوسط فالتقدير (20) هو القيمة الرقمية للمقدر والمحسوبة من بيانات العينة، ومثال آخر لتقدير النسبة الحقيقية P
^ ^
للناخبين المؤيدين لمرشح في الانتخابات فكانت P نسبة الناخبين في العينة لمؤيدي هذا المرشح ومن ثم قمنا بسحب عينة عشوائية من 1000 شخص فوجد أن P =ـ0.45
فتعتبر مقدر نقطة لنسبة المجتمع P في حين تعتبر القيمة 0.45 تقديراً لها. وقد تختلف قيمة المقدر عن قيمة معلمة المجتمع المجهولة والقول بالتساوي قولاً خطئا ولكن كلما كبر حجم العينة فإن قيمة المقدر تقترب لقيمة معلمة المجتمع المجهولة وحسن استغلال الوقت ولاستخدام البيانات بكفاءة فلا بد التعرف على خصائص مقدر النقطة الجيد وهي:
عدم التحيز ( Unbiasedness ) الكفاءة ( Efficiency ) التوافق أو الاتساق ( Consistency )