عدم التحيز ( Unbiased ness ):
إن الإحصائية تكون مقدراً غير متحيز للمعلمة عندما يكون متوسط توزيع المعاينة الإحصائية يساوي معلمة المجتمع المقابلة وألا فيسمى مقدراً متحيز فمثلاً إن تقدير الوسط
ــــ
الحسابي X للعينة المسحوبة عشوائياً من مجتمع مساوياً μ الوسط الحسابي للمجتمع عندها يكون التقدير غير متحيز أي أن:
ــــ ــــ ـــ
E( X ) = μ أي E( X ) – μ = 0 نقول أن X مقدر نقطة غير متحيز لمتوسط المجتمع μ.
^ ^
يمكن تعميم ذلك على أي معلمة Ө ولأي إحصاءه تعود لعينة Ө فالتقدير غير المتحيز يكون: E( Ө ) = Ө ـ
وتجدر الإشارة هنا بحصول التقدير غير المتحيز بتقديرات لتجارب متعددة وليس بقيمة واحدة.
مثـال:
لدينا 12 شخص يمتلكون المبالغ التالية مرتبين تصاعدياً ( بآلاف الدنانير ) 1، 3، 4، 5، 5، 6، 7، 9، 10، 11، 11، 12 وسحبت عينة منتظمة واحدة من أربع مبالغ، وضح العينات الممكن سحبها ومتوسط كل منها ومن ثم أثبت أن تقدير متوسط المجتمع غير متحيز.
الحــل:
إن حجم
العينة المناسب في حالة السحب هو
| العينات الممكن سحبها | المفردات | المتوسط الحسابي |
| x1 | 1 , 5 , 7 , 11 | 6 |
| x2 | 3 , 5 , 9 , 11 | 7 |
| x3 | 4 , 6 , 10 , 12 | 8 |
نريد إثبات أن هذه المتوسطات (للعينات) مقدر غير متحيز لمتوسط المجتمع أي:
![]()
نعلم أن احتمال العينة يساوي عدد أفرادها على كل المفردات أي 4 ÷ 14 فنحسب المتوسط الموزون لوجود أكثر من عينة أي أن:
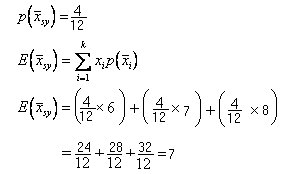
ولحساب متوسط المجتمع نجد أن:
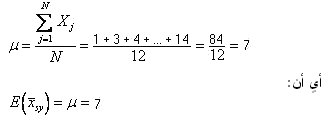
أي أن متوسط توزيع المعاينة الإحصائية (7) يساوي معلمة المجتمع المقابلة (7) وعليه يكون تقدير متوسط المجتمع غير متحيز.