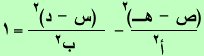القطوع المخروطية (ملخص)

الدوال الزائدية للقطع

القطـع الزائـد / نشأته وإيجاد معادلته( البرهـان )

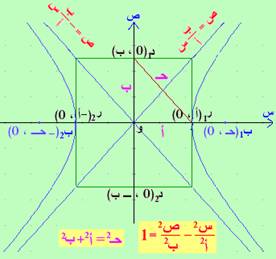
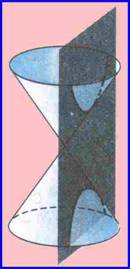
تعريف : هو المحل الهندسي لنقطة تتحرك في المستوى بحيث تكون القيمة المطلقة للفرق بين بعد كل منها عن نقطتين ثابتتين في المستوى مساويا مقدار ثابت . وتعرف النقطتين الثابتتين ببؤرتي القطع الزائد ومركز القطع الزائد أما نقطة الأصل (0،0) أو أي نقطة في المستوى (د ، هـ ) بنقل المحاور إليها من نقطة الأصل

الجدولين الآتيين ملخص عن القطع الزائد في حالتي المركز ( 0 ، 0 ) ، ( د ، هـ )

( 0 ، 0 ) نقطة الأصل		المركز
		معادلة القطع القياسية
يقع على المحور الصادي	يقع على المحور السيني	المحور الأكبر

البؤرتان	( حـ ، 0 )	(- حـ ، 0)	(0 ، حـ)	(0 ، - حـ)
الرأسان	( أ ، 0 )	(- أ ، 0 )	(0 ، أ )	(0 ، - أ )
الخطوط التقاربية
محورا التناظر	محور الصادات( س = 0 ) ، محور السينات( ص = 0 )

( د ، هـ ) أي نقطة في المستوى		المركز
		معادلة القطع القياسية
موازي المحور الصادي	موازي المحور السيني	المحور الأكبر

البؤرتان	(د + حـ ، هـ)	(د - حـ ، هـ)	( د ، هـ + حـ)	( د ، هـ - حـ)
الرأسان	( د + أ ، هـ )	( د - أ ، هـ )	( د ، هـ + أ )	( د ، هـ - أ )
الخطوط التقاربية
محورا التناظر	س = د (موازي محور الصادات) ، ص = هـ (موازي محور السينات)

بعد التقديم السابق يجب الاهتمام بالجدول مع أن الجدول الثاني ناتج من الجدول الأول بنقل للنقطة (د ، هـ) مركز القطع فالعملية هي عملية جمع ، لاحظ البؤرة في الجدول الأول (0 ، أ) أضف (د ، هـ) تنتج البؤرة (د ، هـ + أ) المناظرة في الجدول الثاني وكذلك الرأس في الأول ( أ ، 0 ) فأضف ( د ، هـ ) ينتج ( د + أ ، هـ ) المناظر له في الجدول الثاني وقس على ذلك مع أن هذا ليس علماً بقدر ما هو تسهيلاً لإجراء عمل ما

ومعادلة القطع الزائد في الجدول الثاني تؤول إلى الصورة ل س² + ك ص² + ن س + ى ص + م = 0 حيث ل ك < 0 أي ل ، ك مختلفا الإشارة وهي المعادلة العامة للقطع الزائد ويجب استخدام إكمال المربع أو أي طريقة أخرى لوضعها بإحدى الصور السابقة لمعرفة أ ، ب ومنها حـ حيث حـ² = ا² + ب²

إن النسبة حـ : أ تسمى الاختلاف المركزي للقطع الزائد ويرمز لها بالرمز e حيث 0 < e < 1

4س² – 16 س + ص²+2 ص - 19 = 0 ترتيب

4(س²- 4 س) –(ص² + 2 ص) - 19 = 0 تجميع

4(س²-4 س + 4 - 4 )– (ص² + 2 ص + 1-1)-19 =0 إضافة

4(س - 2)² - 16 – (ص + 1)²-1-19=0 مربع كامل وتجميع

4(س - 2)² – (ص + 1)² - 36 = 0 نقل

4(س - 2)² – (ص + 1)² = 36 القسمة على 36

هذه معادلة قطع زائد مركزه (2 ، ـ1) محوره يوازي محور السينات

أ² = 9 فإن أ = 3 ، ب² = 36 فإن ب = 6 ،

حـ² = 9 + 36 = 45 فإن حـ = 3(5)^½

الرأسان هما ( 3+2 ، -1) ، ( -3+2 ، -1) أي (5 ، -1) ، ( -1 ، -1)

البؤرتان هما (3(5) ^½ + 2 ، -1) ، (-3(5) ^½ +2 ، -1)

الخطوط التقاربية هما (ص + 1) = 2( س ـ 2) ، (ص + 1) = ـ 2(س ـ 2) أي ص ـ 2 س + 5 = 0 ، ص + 2 س ـ 3 = 0

الاختلاف المركزي هو حـ : أ أي 3(5)^½ : 3 أي (5) ^½

لاحظ :

1) العلاقة بين أ ، ب ، حـ هي حـ² - أ² = ب² ولا توجد علاقة بين أ ، ب كما هي في القطع الناقص يكون أ > ب

2) الخطوط التقاربية للقطع لا تقطع المحور الصادي إلا في ما لانهاية

3) معادلات الخطوط التقاربية تنتج من المعادلة القياسية للقطع فمثلاً

س²/أ2 - ص²/ب² = 1

ص² = ب² ( س²/أ² – 1 )

= ب²/أ² ( س² – أ² )

ص= ± ب/أ ( س² – أ² ) ^½

ص= ± (ب/أ)س ( 1 – أ²/ س²) ^½ عندما س تؤول إلى ما نهاية فإن أ²/ س² يؤول للصفر ، ص = ± (ب/أ)س

مثال آخر

مع تمنياتي بالتوفيق وملاحظاتكم تطوير للموجود ...................... محمد شكري الجماصي