أدرس المعادلة 4س2
- ص2
- 6س
- 2ص + 11 = صفر وارسم المنحنى الذي تمثله
نرتب المتغيرات
4 س2 – 6 س – ص2 – 2 ص + 11 = 0
نجعل معامل س2 ، ص2 الوحدة (1) غالباً ما يكون بأخذ المعامل كعامل مشترك
4(س2
– 1.5س) – (ص2 +2ص) + 11 =0
نضيف
داخل القوسين حد ثالث مربع نصف معامل س أو ص ونطرح نفس الكمية ¾ ، 1
4(س2
– 1.5س + (¾)2 - (¾)2) – (ص2 + 2ص + 1 - 1) + 11
=0
نكون
المربع الكامل للحدود الثلاثة في الأقواس
4[(س – 1.5)2
- (¾)2] – [(ص + 1)2 –1] + 11 = 0
بفك
الأقواس الكبيرة فقط
4(س – 1.5)2
– 4×(¾)2 – (ص + 1)2 + 1 + 11 = 0
نجمع الثابت وننقله للطرف الأيسر – 4×(¾)2 + 1 + 11 = 39/4
4(س – 1.5)2
– (ص + 1)2 = - 39/4
نقسم
على-39/4 مع نقل4المرفقة مع القوس الأول للمقام ولاحظ تغير إشارة القوسين
(ص + 1)2
/ (39/4) - (س – 1.5)2
/(39/16) = 1
نوجد أ، ب، حـ فيكون
أ =(جذر39)/2 ≈ 3.1 ، ب = (جذر39)/4 ، حـ2 = أ2+ب2
= 195/16 ، حـ ≈ 4 وعليه يكون
مركز القطع (د
، هـ) أي
مركز القطع
(1.5 ، -1)
الرأسان ( د ،
هـ + أ ) ، ( د ، هـ - أ ) أي
الرأسان (1.5
، -1+3.1)، (1.5 ، -1-3.1) أي (1.5 ، 2.1) ، ( 1.5 ، -4.1)
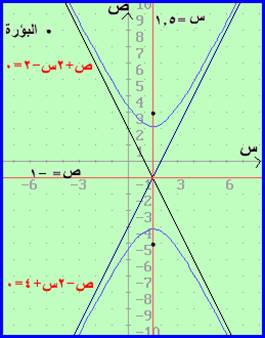
البؤرتان ( د ،
هـ + حـ ) ، ( د ، هـ - حـ ) أي
البؤرتان (1.5
، -1 + 4)، (1.5 ، -1 – 4 ) أي (1.5 ، 3 ) ، ( 1.5 ، - 5)
محورا التناظر
هما س = د ، ص = هـ أي
محورا التناظر هما س = 3/2 ،
ص = -1
الخطوط التقاربية : لاحظ أ /ب = (جذر39)/2 × 4/(جذر39) = 2
الخطوط التقاربية هي ص – هـ = ± (أ/ب) ( س – د) أي
الخطوط
التقاربية هي ص +1 = 2 ( س – 1.5) ، ص +1 = -2 ( س – 1.5) أي
الخطوط
التقاربية هي ص +1 = 2س – 3 ، ص +1 = -2س + 3 أي
الخطوط
التقاربية هي ص – 2س + 4 = 0 ، ص + 2س - 2 = 0
الاختلاف
المركزي حـ/أ أي
الاختلاف
المركزي 4/((جذر39)/4)) = 16/(جذر39) ≈ 2.6
الرســـم