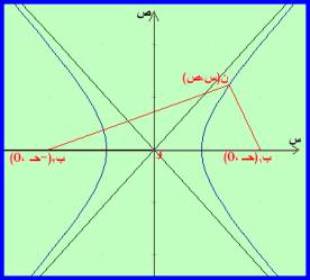
الشكل يمثل قطع زائد مركزه
نقطة الأصل و( 0 ، 0 ) ، ن(س ، ص) إحدى نقطه
|
|
| ن ب2 ـ
ن ب1 | = ثابت
بافتراض
الثابت = 2 أ
| ن ب2 ـ ن ب1 | = 2 أ
أما ن ب2
ـ ن ب1 = 2 أ
أو ن ب1 ـ ن ب2 = 2 أ
من الشكل يكون
ن ب2 ـ ن ب1 = 2 أ حيث ن ب2 >
ن ب1 (1)
نحصل على ن ب1،
ن ب2 من قانون البعد بين نقطتين
ن
ب1 = [(س– حـ)2+ص2]½
ن ب2
= [(س+حـ)2+ص2]½
بالتعويض
في (1)
[(س+حـ)2+ص2]½ - [(س– حـ)2+ص2]½ =2أ
[(س+حـ)2+ص2]½ =2أ + [(س– حـ)2+ص2]½
بالتربيع نحصل على
(س + حـ)2
+ ص2 = 4 أ2 + 4أ [(س – حـ) + ص2]½ + (س – حـ)2
+ ص2
س2+2
حـ س+حـ2+ص2=4 أ2+ 4أ [(س
– حـ)2 + ص2]½ +
س2-2
حـ س+ حـ2 + ص2
4أ [(س – حـ)2 + ص2]½ =4 حـ س - 4 أ2
بالقسمة على 4
أ [(س – حـ)2 + ص2]½ = حـ س - أ2 بالتربيع
أ2(س2-
2حـ س +
حـ2+ ص2)
= حـ2 س2 –2 حـ
س أ2 +
أ4
أ2 س2 - 2أ2حـ س
+ أ2 حـ2 + أ2 ص2 = حـ2
س2 –
2أ2حـ س +
أ4
حـ2
س2 - أ2 س2 - أ2 ص2 = أ2
حـ2 - أ4
س2(حـ2
- أ2) - أ2 ص2 = أ2(حـ2 -
أ2) ---(2)
لكن 2 حـ > 2 أ فإن حـ > أ أي حـ2 > أ2
بوضع حـ2
- أ2 = ب2 فتؤول المعادلة (2) إلى
ب2 س2
- أ2 ص2 = ا2 ب2 وبالقسمة على ا2
ب2
![]()
المعادلة
القياسية للقطع الزائد الذي مركزه (0 ، 0) وتقع بؤرتاه على محور السينات
بوضع ص = 0
نحصل على س = أ ، س = - أ
الإحداثيات السينية لطرفا المحور الأساسي(الرئيسي)
تسمى النقطتان
(أ ، 0) ، (- أ ، 0) رأسي القطع الزائد وهما نقطتا تقاطع القطع مع محور السينات
بوضع س = 0 لا
نحصل على قيم حقيقية للمتغير ص فمنحنى القطع الزائد لا يقطع محور الصادات
طول المحور الأساسي(الرئيسي)=
2 أ ، طول المحور الفرعي(الثانوي) = 2 ب
القطع متناظر
حول كل من محور الصادات و محور السينات
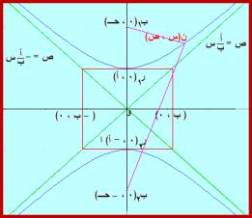
الشكل
الثاني البؤرتان على محور الصادات ومعادلة القطع هي
![]()