الاتجاهات غير الخطية Non Linear Trends

    ذكرنا سابقاً الاتجاه الخطي وصورته Y = a + bX وقد يكون وصف التغيرات في السلسلة لا يمكن استخدام المعادلة الخطية وخاصة لتلك السلسلة ذات الأمد الطويل فتكون المعادلة غير الخطية أفضل لقياس منحنى الاتجاه العام T وتوجد عدة طرق لقياس أثر الاتجاه العام في حالة الاتجاه غير الخطي ومن بينها معادلة الاتجاه التربيعية (القطع المكافئ) أو معادلة الدرجة الثانية ، معادلة الاتجاه الأسي وأخرى.

معادلات الاتجاه ألتربيعي Quadratic Trend Equations:                معادلات الاتجاه الأسي                معادلات اتجاهية أخرى

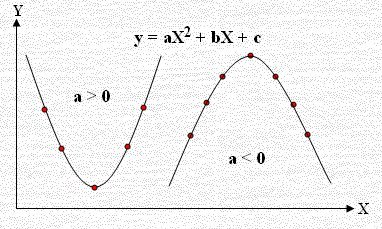
    سبق أن ذكرنا معادلة الانحدار ألتربيعي Quadratic Regression Equations ومعادلة الاتجاه ألتربيعي تأخذ شكل القطع المكافئ كما مبين بالشكل (مفتوح من أعلى أو من أسفل) أو مفتح جهة اليمين أو جهة اليسار ومعادلته هي:

Ŷ = a + bX + c X2

وحيث أن X = t – `t فبوضعها في المعدلة نحصل على:

Ŷ = a + b ( t – `t ) + c( t – `t )2

ونحسب قيم الثوابت a, b , c بطريقة المربعات الصغرى السابق ذكرها فبإجراء عملية الجمع المتكرر للمعادلة Ŷ = a + bX + cX2 نحصل على المعادلات الثلاث الآتية:

 ∑Y = na + b∑X + c ∑X2

 ∑XY = a∑X + b∑X2 + c ∑X3

 ∑X2Y = a∑X2 + b∑X3 + c ∑X4

بحل هذه المعادلات بالطرق الرياضية أو الحاسوب نحصل على قيم الثوابت وإذا أخذنا قيم إلى X مجموعها يساوي صفر أي: X = 0∑ فإن  X3 = 0∑ وتكون قيم الثوابت للمعادلات الآتية:

 ∑Y = na + c ∑X2

 ∑XY = b∑X2 + c ∑X3

 ∑X2Y = a∑X2 + c ∑X4

هي:

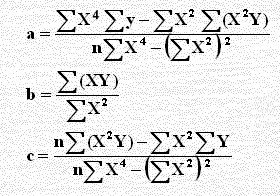
مثال:

    الجدول التالي يبين عدد الطلاب الجدد لأحد المدارس الخاصة في السنوات 1991ــ 1999. أوجد معادلة الاتجاه ألتربيعي ومثلها بيانياً.

 

1999 1998 1997 1996 1995 1994 1993 1992 1991 السنة
4 3 2 1 0 – 1 – 2 – 3 – 4 X
98 94 95 94 93 94 89 88 85 عدد الطلاب Y

الحل:

    نكون جدول للبيانات المطلوبة لإيجاد قيم a, b , c وهو كالتالي:>

 X2Y  XY  X4 X2 Y X السنة
1360 – 340 256 16 85 – 4 1991
792 – 264 81 9 88 – 3 1992
356 – 178 16 4 89 – 4 1993
94 – 94 1 1 94 – 1 1994
 0 0 0 0 93 0 1995
 94 94 1 1 94 1 1996
 380 190 16 4 95 2 1997
 846 282 81 9 94 3 1998
 1568 392 256 16 98 4 1999
5490 82 708 60 830 0 Total

 

بتطبيق الصيغ السابقة نجد أنَّ:

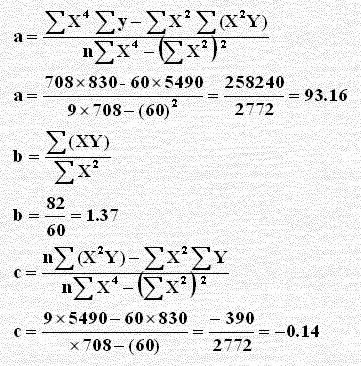
معادلة الاتجاه ألتربيعي هي:

Ŷ = a + bX + c X2

Ŷ = 93.16 + 1.37X – 0.14 X2

والتمثيل البياني لهذه المعادلة (الدالة) في صورتها العامة كالآتي مع أن رأس القطع تقريباً هو ( 5 ، 96.5) باعتبار أن:

ألإحداثي السيني =  – ( 1.37 ÷ 2 ×  – 0.14) = 4.89 ≈ 5

وبالتعويض في المعادلة نجد أن قيمة ألإحداثي الصادي = 93.16 + 1.37 × 5  – 0.14 × 25 = 96.5

رأس القطع ( 5 ، 96.5 )

 

 

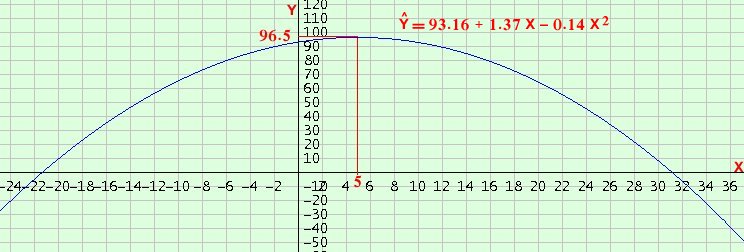
للتمثيل البياني للاتجاه ألتربيعي نأخذ t`t = 1995وتصبح المعادلة Ŷ = 93.16 + 1.37X – 0.14 X2 الصورة الآتية:

 Ŷ = 93.16 + 1.37( t – `t )  – 0.14 ( t – `t ) 2

فمثلاً سنة 1991:

 Ŷ = 93.16 + 1.37(1991 – 1995) – 0.14 (1991 – 1995) 2

   = 93.16 + 1.37 × 4 – 0.14 × (4)2

   = 93.16 + 5.46 – 2.24

  = 88.44

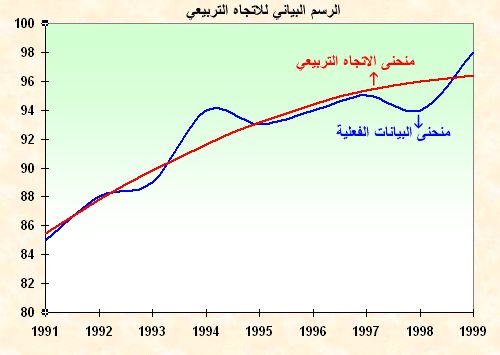
نكرر التعويض عن كل سنة t من سنوات السلسلة الزمنية (1991 ـ 1999) والقيم الناتجة ( لاحظ الجدول أدناه) يمكن تمثيلها كما في الشكل الآتي مع البيانات الفعلية:

 

 

عنصر الاتجاه t
 85.44 1991
 89.79 1992
 89.86 1993
 91.65 1994
 93.16 1995
 94.39 1996
 95.34 1997
 96.34 1998
 96.40 1999