معادلات الاتجاه الأسي Exponential Trend Equations
يستخدم هذا النوع من المعادلات لقياس الاتجاهات ذات نسب التغير السنوي الثابتة وتستخدم المعادلة النصف اللوغاريتمية لبحث حالة الاتجاه يزداد أو يتناقص بنسبة مئوية سنوية ثابتة ويكون الاتجاه أسي حال تبيان الاتجاه للسلسلة خط مستقيم والصورة لمعادلة الاتجاه الأسي حيث t السنة ، t`متوسط السلسلة فإن X = t –`t فإن المعادلة:
Y1 = d(1+i)( t –`t ) Or
Y1 = d(1+i)X بأخذ اللوغاريتم الطبيعي
Lin Y1 = Lin d + X Lin (1+i)
وهي معادلة لوغاريتمية خطية يمكن استخدام طريقة المربعات الصغرى للحصول على القيم d , 1+i من الصيغتين الآتيتين:
Lin d = (∑LinY)/n → (1)
Lin(1 + i) = (∑XLinY)/∑X2 → (2)
مثال:
الجدول التالي يبين عدد الطلاب الجدد لأحد المدارس الخاصة في السنوات 1991ــ 1999. أوجد الاتجاه الأسي وعدد الطلبة الجدد المتوقع سنة 2007 ومثلها بيانياً.
| 1999 | 1998 | 1997 | 1996 | 1995 | 1994 | 1993 | 1992 | 1991 | السنة |
| 4 | 3 | 2 | 1 | 0 | – 1 | – 2 | – 3 | – 4 | X |
| 98 | 94 | 95 | 94 | 93 | 94 | 89 | 88 | 85 | عدد الطلاب Y |
من البيانات نجد أن n = 9 ، ومتوسط السنوات هو t`ويساوي 1995 ولإيجاد المطلوب نكون جدول البيانات التالي:
| X LinY | LinY | X2 | Y | X | السنة |
| – 17.7706 | 4.4427 | 16 | 85 | – 4 | 1991 |
| – 13.4320 | 4.4773 | 9 | 88 | – 3 | 1992 |
| – 8.9773 | 4.4886 | 4 | 89 | – 4 | 1993 |
| – 4.5433 | 4.5433 | 1 | 94 | – 1 | 1994 |
| 0.0000 | 4.5326 | 0 | 93 | 0 | 1995 |
| 4.5433 | 4.5433 | 1 | 94 | 1 | 1996 |
| 9.1078 | 4.5539 | 4 | 95 | 2 | 1997 |
| 13.6299 | 4.5433 | 9 | 94 | 3 | 1998 |
| 18.3399 | 4.5850 | 16 | 98 | 4 | 1999 |
| 0.8976 | 40.710 | 60 | 830 | 5 | Total |
نستخدم الصيغ (1) ، (2) أعلاه لحساب القيم المطلوبة
Lin d = (∑LinY)/n
= 40.71 / 9
= 4.5233
d = 92.1392 ≈ 92.12
Lin(1 + i) = (∑XLinY)/∑X2
= 0.8976 / 60
= 0.015
1 + i = 1.0151 ≈ 1.02
i = 0.0151 ≈ 1.02
معدل النمو السنوي i = 0.0151 أي النسبة المئوية للزيادة في عدد الطلاب الجدد هي 0.0151 × 100 = 1.51% والمعادلة الاتجاه الأسي هي:
Y1 = d(1+i)( t –`t )
Y1 = 92.12(1.02)( t – 1995)
عدد الطلاب الجدد المتوقع سنة 2007
Y1 = 92.12(1.02)( 2007 – 1995)
Y1 = 92.12(1.02)12
Y1 = 92.12× 1.2682
Y1 = 117
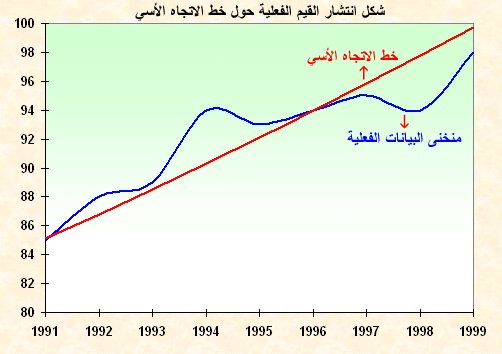
نكرر التعويض عن كل سنة t من سنوات السلسلة الزمنية (1991 ـ 1999) والقيم الناتجة قربت لعدد صحيح ( لاحظ الجدول أدناه) يمكن تمثيلها كما في الشكل التالي والذي يبين شكل انتشار القيم الفعلية حول خط الاتجاه الأسي:

| عنصر الاتجاه | t |
| 85 | 1991 |
| 87 | 1992 |
| 89 | 1993 |
| 90 | 1994 |
| 92 | 1995 |
| 94 | 1996 |
| 96 | 1997 |
| 98 | 1998 |
| 100 | 1999 |