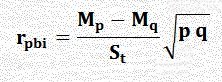
معامل الارتباط ثنائي التسلسل (Point Biserial Correlation Coefficient) تفسير ومثال آخر
يقيس قوة العلاقة بين فقرة السؤال والدرجة الكلية للاختبار حيث يكون تصنيف الفقرة في السؤال ثنائي ( s0 , 1) في حين درجة الامتحان الكلية كمتغير مستمر وقانونه:
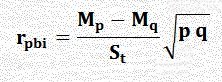
حيث Where
|
rpbi معامل الارتباط ثنائي التسلسل |
rpbi point-biserial correlation coefficient |
|
Mp متوسط الإجابات الصحيحة للطلاب في فقرة السؤال يرمز s1 |
Mp whole-test mean for students answering item correctly |
|
Mq متوسط الإجابات الغير الصحيحة للطلاب في فقرة السؤال يرمزs0 |
Mq whole-test mean for students answering item incorrectly |
|
St الانحراف المعياري لدرجات الاختبار |
St standard deviation for whole test |
|
p احتمال الإجابة الصحيحة للطلاب ترمز برقم s1(النسبة المئوية √ ) |
p proportion of students answering correctly |
|
q احتمال الإجابة الخاطئة للطلاب ترمز برقم s0 ( النسبة المئوية X ) |
q proportion of students answering incorrectly |
أو القانون:
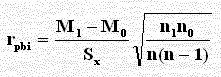
حيث أن n1 عدد البيانات في مجموعة الأولى ، n2 عدد البيانات في مجموعة الثانية ، n = n1 + n2
مثال:
الجدول التالي (الأعمدة عدا L والصفوف من 1i إلى i11) يبين إجابات تسعة طلاب في اختبار مكون من عشرة فقرات حيث أعطيَّ s1للإجابة الصحيحة ، s0للإجابة الخاطئة احسب عامل الارتباط ثنائي التسلسل باستخدام برنامج EXCEL ، القوانين أعلاه، SPSS، MINITAB
أولاً: باستخدام برنامج Excel ثانياً: باستخدام القوانين ثالثاً: باستخدام برنامج SPSS رابعاً: باستخدام MINITAB
جدول البيانات المعطى تم إضافة العمود L مجموع الإجابات والصف i 12 كمجموع والأعمدة التالية ناتج طرح قيم العمود L من القيم المقابلة له (الأعمدة A, B , ..., K) فمثلاً:
قيم العمود B15:B24 ناتج طرح قيم العمود L من قيم العمود B من صف i2 إلى صف i11 مثل L2 – B2
| L | K | J | I | H | G | F | E | D | C | B | A | |
| Total | Item10 | Item9 | Item8 | Item7 | Item6 | Item5 | Item4 | Item3 | Item2 | Item1 | Name | 1 |
| 9 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
ALI |
2 |
| 8 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
SALEM |
3 |
| 7 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 |
AHMED |
4 |
| 7 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
JAMAL |
5 |
| 5 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 |
MOOSE |
6 |
| 5 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
FATHER |
7 |
| 5 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
MUSTAFA |
8 |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
YEANS |
9 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
SÁMI |
10 |
| 2 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
JAMUL |
11 |
| 55 | 2 | 3 | 3 | 5 | 6 | 5 | 7 | 8 | 8 | 8 | TOTAL | 12 |
| 13 | ||||||||||||
| Item10 | Item9 | Item8 | Item7 | Item6 | Item5 | Item4 | Item3 | Item2 | Item1 | Name | 14 | |
| 9 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 |
ALI |
15 | |
| 7 | 7 | 7 | 7 | 7 | 8 | 8 | 7 | 7 | 7 |
SALEM |
16 | |
| 6 | 6 | 6 | 6 | 6 | 7 | 6 | 7 | 6 | 7 |
AHMED |
17 | |
| 7 | 7 | 7 | 6 | 6 | 6 | 6 | 6 | 6 | 6 |
JAMAL |
18 | |
| 5 | 5 | 5 | 4 | 4 | 4 | 5 | 4 | 5 | 4 |
MOOSE |
19 | |
| 5 | 5 | 5 | 5 | 4 | 5 | 4 | 4 | 4 | 4 |
FATHER |
20 | |
| 5 | 5 | 5 | 5 | 5 | 4 | 4 | 4 | 4 | 4 |
MUSTAFA |
21 | |
| 4 | 4 | 4 | 4 | 4 | 4 | 3 | 3 | 3 | 3 |
YEANS |
22 | |
| 3 | 3 | 3 | 3 | 3 | 3 | 2 | 2 | 2 | 3 |
SÁMI |
23 | |
| 2 | 2 | 2 | 2 | 2 | 1 | 2 | 2 | 2 | 1 |
JAMUL |
24 | |
|
القيم في الصف التالي نتجت من برنامج EXCEL بكتابة CORREL(B2:B11;B15:B24)s= في الخانة الأولى (s– 0.07) ثم نسخها لباقي الخانات |
25 | |||||||||||
| 0.31 | 0.66 | 0.66 | 0.69 | 0.65 | – 0.19 | – 0.06 | 0.05 | 0.31 | – 0.07 |
BiSearial |
26 | |
|
القيم في الصف التالي تبين الاحتمال لكل فقرة، ناتج الخانة الأولى من قسمة المجموع على حجم العينة أي s8 ÷ 9= 0.89وتنسخ لباقي الخانات |
27 | |||||||||||
| 0.22 | 0.33 | 0.33 | 0.56 | 0.67 | 0.56 | 0.78 | 0.89 | 0.89 | 0.89 |
Pvalue |
28 | |
القيم السالبة ترفض (وجود خطأ ما)
أولاً نحسب الانحراف المعياري St ( الجدول التالي) حيث أن:
Mp = (8+7+6+4+4+4+3+1)/8 = 37 / 8 = 4.625
Mq = (7 + 3) / 2 = 5
Mp – Mq = – 0.375
P = 8 / 10 = 0.8
q = 2 / 10 = 0.2
![]()
| (M – Total)2 | M – Total | Total – Item1 | Total | Item1 | Name |
| 18.49 | 4.7 – 8 = – 4.3 | 9 – 1 = 8 | 9 | 1 |
ALI |
| 10.98 | – 3.3 | 8 – 1 = 7 | 8 | 1 |
SALEM |
| 5.29 | – 2.3 | 7 | 7 | 0 |
AHMED |
| 5.29 | – 2.3 | 6 | 7 | 1 |
JAMAL |
| 0.09 | – 0.3 | 4 | 5 | 1 |
MOOSE |
| 0.09 | – 0.3 | 4 | 5 | 1 |
FATHER |
| 0.09 | – 0.3 | 4 | 5 | 1 |
MUSTAFA |
| 0.49 | 0.7 | 3 | 4 | 1 |
YEANS |
| 2.89 | 1.7 | 3 | 3 | 0 |
SÁMI |
| 7.29 | 2.7 | 1 | 2 | 1 |
JAMUL |
| 50.9 | M = 47 / 10 = 4.7 |
Total |
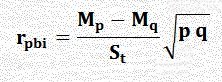
= – 0.375 × 0.4 ÷ 2.256
= – 0.07
OR
n1 = 8 عدد الإجابات الصحيحة
n2 = 2 عدد الإجابات الخاطئة
n = 10 العدد الكلي
n1 n2 / n(n – 1) = 16 / 90 = 0.178
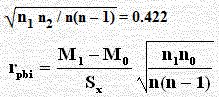
= – 0.375 × 0.422 ÷ 2.256
= – 0.07
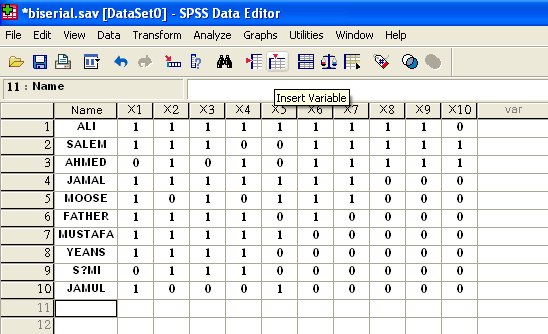
1) يتم إدخال البيانات للطلاب العشرة (المبينة أسمائهم في عمود المتغير Name مع نتائجهم في الفقرات العشرات المبينة بالمتغيرات من X1 إلى X10
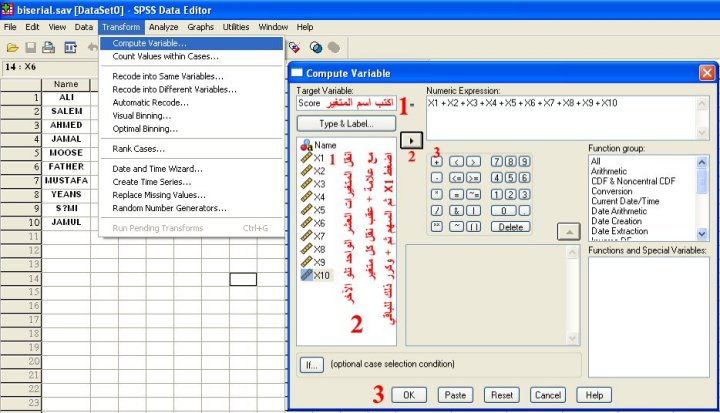
2) نوجد مجموع درجات كل طالب بالمتغير Score كما مبين بالشكل التالي:
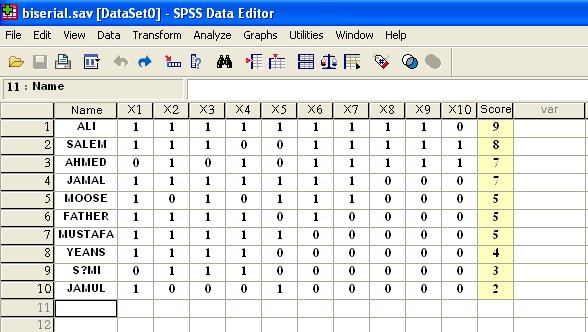
فنحصل على المجموع تحت اسم للمتغير الجديد Score كما مبين بالشكل:
3) نضيف متغيرات جديدة Y10 ، ... ، Y1 بإيجاد الفرق بين Score والمتغير الأول X1 ضمن المتغير الجديد Y1 بنفس الطريقة الموضحة بالشكل قبل السابق بدل الجمع
نختار المتغير Score ثم – ثم X1 مع تكرار ذلك للمتغيرات الجديدة الأخرى كالتالي:
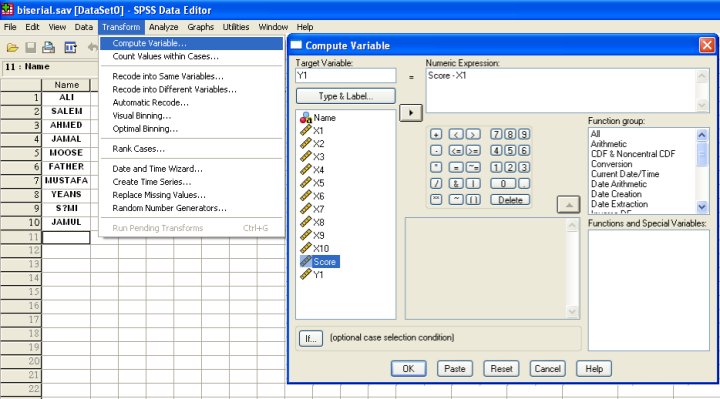
4) في شاشة البيانات نجد الآتي:
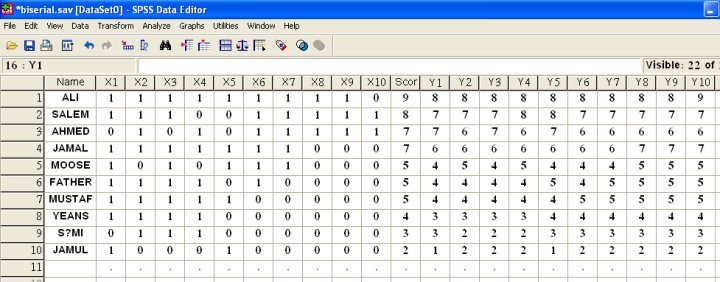
5) نحلل البيانات حسب الشكل التالي:
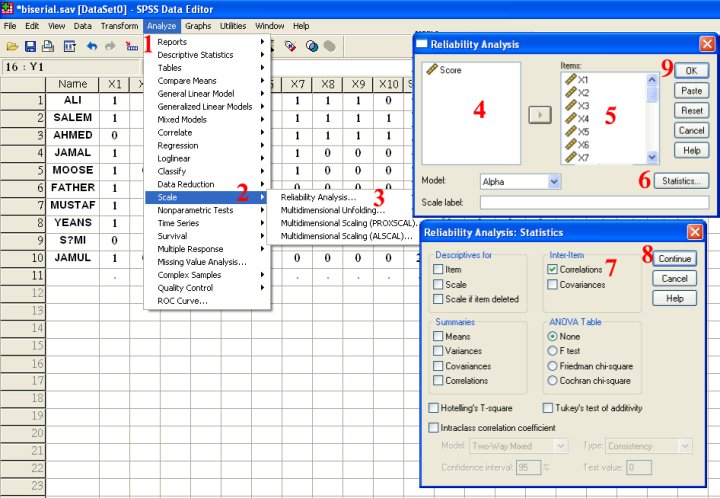
6) نجد نتيجة التحليل في مخرجات SPSS كالتالي بعد تنسيقها:
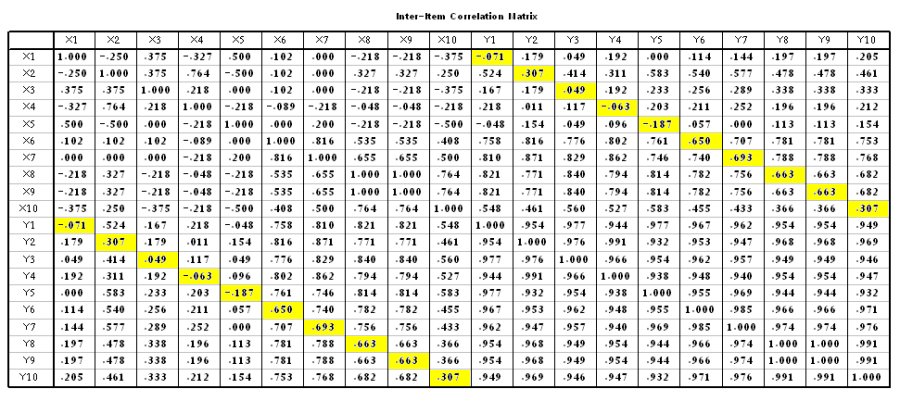
وهي نفس النتائج السابقة.