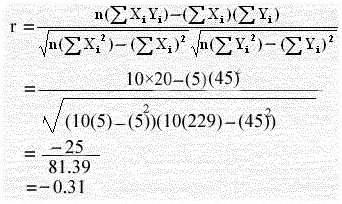معامل بوينب بايسيريال / Point-Biserial
معامل ارتباط ثنائي متسلسل Biserial Correlation يستخدم لإيجاد درجة العلاقة بين متغيرين فالأول ثنائي حقيقي X والثاني كمي متصل Y ويفترض في المتغيرالثنائي أن يكون منتظماً في كلا التقسيمين (كمجموعة الناجحين (1) , مجموعة الراسبين (0)) أي متكافئون في النجاح والرسوب مثلاً ونستخدم المعادلة الآتية لحساب rpb معامل ارتباط بوينت بايسيريال

حيث:
1) نقسم المتغير X لمتغيرين كميين حسب مستويات Y ويكون Y1 للنجاح مثلاً أو للإجابة بنعم (المستوى الأول) , Y0 للرسوب مثلاً أو للإجابة بلا (المستوى الثاني).
−
2) Y1 يمثل المتوسط تحت المستوى الأول (المجموعة التي حصلت على الواحد الصحيح).
−
3) Y0 يمثل المتوسط تحت المستوى الثاني (المجموعة التي حصلت على الصفر).
4) SY يمثل الانحراف المعياري للمتغير Y
5) n عدد المشاعدات الكلي , n1 عدد مشاعدات المستوى الأول , n0 عدد مشاعدات المستوى الثاني.
مثال: أوجد الارتباط بين الدرجة الكلية في اختبار اختيار من متعدد Y ودرجة احدى فقرات الاختيار X لمجموعة مكونة من i10طلاب حسب الجدول التالي:
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | X |
| 7 | 6 | 6 | 4 | 4 | 5 | 5 | 4 | 3 | 1 | Y |
الحل:
1) نحسب متوسط الدرجات الكلية للمجموعة الحاصلة على الواحد الصحيح : Y\1 = i(1 + 3 + 5 + 5 + 6) ÷ 5 = 20 ÷ 5 = 4
2) نحسب متوسط الدرجات الكلية للمجموعة الحاصلة على الصفر : Y\0 =i(4 + 4 + 4 + 6 + 7) ÷ 5 = 25 ÷ 5 = 5
3) نحسب متوسط الدرجات الكلية : Y\ = i(1 + 3 + 4 + 5 + 5 + 4 + 4 + 6 + 6 + 7) ÷ 10 = 45 ÷ 10 = 4.5
4) نحسب الانحراف المعياري بإكمال الجدول التالي ومنهiSY2 = Σ(Y-Y\)2 ÷ n i أي SY2 = 26.5 ÷ 10 = 2.65 ومنها نأخذ الجذر التربيعي أي: SY = 1.63
| X | Y | Y-Y\ | (Y-Y\)2 |
| 1 | 1 | -3.5 | 12.25 |
| 1 | 3 | -1.5 | 2.25 |
| 0 | 4 | -0.5 | 0.25 |
| 1 | 5 | 0.5 | 0.25 |
| 1 | 5 | 0.5 | 0.25 |
| 0 | 4 | -0.5 | 0.25 |
| 0 | 4 | -0.5 | 0.25 |
| 0 | 6 | 1.5 | 2.25 |
| 1 | 6 | 1.5 | 2.25 |
| 0 | 7 | 2.5 | 6.25 |
| 5 | 45 | 26.50 |
5) نطبق معادلة بوينت بايسيريال السابقة:
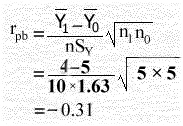
—————————————
ومن حيث أن معادلة بوينت بايسيريال حالة خاصة من معادلة الارتباط لبيرسون فبالإمكان حساب معامل ارتباط بيرسون كما يلي:
نكون الجدول الآتي:
| X | Y | X2 | Y2 | X.Y |
| 1 | 1 | 1 | 1 | 1 |
| 1 | 3 | 1 | 9 | 3 |
| 0 | 4 | 0 | 16 | 0 |
| 1 | 5 | 1 | 25 | 5 |
| 1 | 5 | 1 | 25 | 5 |
| 0 | 4 | 0 | 16 | 0 |
| 0 | 4 | 0 | 16 | 0 |
| 0 | 6 | 0 | 36 | 0 |
| 1 | 6 | 1 | 36 | 6 |
| 0 | 7 | 0 | 49 | 0 |
| 5 | 45 | 5 | 229 | 20 |
بتطبيق معادلة الخاصة بمعامل بيرسون للبيانات الأصلية: