1) ما هو نصف المدى الربيعي (Interquartile Range)؟

        هو متوسط الفرق بين الربيعيين الثالث والأول ويعرف أيضاً بالانحراف الربيعي ويرمز له بالرمز Q ويحسب من الصيغة الرياضية:

Q = ½( Q3 – Q1)

        حيث أن البيانات ترتب تصاعدياً أو تنازلياً وتقسم لأربع أقسام نهتم منها بنهاية الربع الأول أو الأدنى (Lawyer Quartile) ويرمز له بالرمز Q1 أي يستبعد الربع الأول وبداية الربع الرابع أو الأعلى (Upper Quartile) ويرمز له بالرمز Q3 أي يستبعد الربع الرابع وهو نحتاج لحسابه Q3 و Q1 عند ربع القيم وثلاثة أرباع القيم كما يبينه الشكل الآتي:     للتفاصيل ehsa/median/med2.htm/

 

2) كيف نحسب نصف المدى الربيعي للقيم غير المبوبة؟

3) كيف نحسب نصف المدر الربيعي للقيم المبوبة؟

4) أذكر مزايا وعيوب نصف المدى الربيعي

        مزاياه: الحصول على مقياس تقريبي للتشتت وللجداول التكرارية ذات الفئات المفتوحة وكذلك حال وجود قيم شاذة

        عيوبه: ليس مقياس دقيق للتشتت بل تقريبي ويستخدم لإعطاء فكرة مباشرة عن التشتت

        هو أفضل من المدى

5) الجدول التالي يبين دخل 500 أسرة  في إحدى المدن والمطلوب إيجاد نصف المدى الربيعي (الانحراف المعياري).

 

Salary 0 – 100 – 200 – 300 – 400 – 500 – 600 – 1000 Total
Family number 22 50 88 120 150 40 30 500

 

أولاً: باستخدام الحساب:

        نكون الجدول المتجمع الصاعد كالآتي:

Intervals (X) Frequency (F)

الحدود العليا للفئات

Upper intervals

التكرار المتجمع الصاعد

Cumulative Frequency (CF)
0 – 22 Less than 100 22
100 – 50 Less than 200 72
200 – 88 Less than 300 160
300 – 120 Less than 400 280
400 – 150 Less than 500 430
500 – 40 Less than 600 470
600 – 30 Less than 1000 500
Total 500    

                   

    ترتيب الربيع الأدنى = 500 ÷ 4 = 125 يقع بين 72 ، 160 (لاحظ الجزء الملون باللون الأصفر) المسافة بينهم 160 – 72 = 88 تناظر في الحدود العليا للفئات قيمة تقع بين 200 ، 300 (لاحظ الجزء الملون باللون الأحمر) المسافة بينهم 200 – 100 = 100 لكن 125 تبعد عن 72 مسافة 125 – 72 = 53 يقابلها قيمة بين 200 ، 300 تساوي 100×53 ÷ 88 = 60.227 أي الربيع الأدنى = 200 + 60.227 = 260.227

توضيح :

 88 ← 100

 53 ← ؟    

؟ = 100×53 ÷ 88 = 60.227   يضاف لبداية الفئة 200 فنحصل على قيمة الربيع الأدنى = 200 + 60.227

                                                                                                                     = 260.227

 

    ترتيب الربيع الأعلى = 3(500 ÷ 4) = 375 يقع بين 280 ، 430 (لاحظ الجزء الملون باللون الأزرق) المسافة بينهم 430 – 280 = 150 تناظر في الحدود العليا للفئات قيمة تقع بين 400 ، 500 (لاحظ الجزء الملون باللون الأزرق) المسافة بينهم 500 – 400 = 100 لكن 375 تبعد عن 280 مسافة 375 – 280 = 95 يقابلها قيمة بين 400 ، 500 تساوي 100×95 ÷ 150 = 63.333 أي الربيع الأدنى = 400 + 63.333 = 463.333

توضيح :

 150 ← 100

95 ← ؟   

؟ = 100×95 ÷ 150 =  63.333  يضاف لبداية الفئة 400 فنحصل على قيمة الربيع الأعلى = 400 + 63.333

                                                                                                                      = 463.333

        نصف المدى الربيعي (الانحراف الربيعي) = ( 463.333 – 260.227 ) ÷ 2 = 203.106 ÷ 2 ≈ 101.5

ثانياً: باستخدام القانون

 

 

 

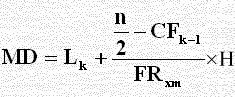
يراجع الوسيط (القانون أعلاه للوسيط والربيعين الأدنى والأعلى بنفس الطريقة)

 

 

                                                                  ترتيب الربيع الأدنى – التكرار المتجمع للفئة السابقة للفئة الربيعية

قيمة الربيع الأدنى = الحد الأدنى  للفئة الربيعية + ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ × طول الفئة      ........ (1)

                                                                                                   تكرار الفئة الربيعية*

* تكرار الفئة الربيعية = التكرار المقابل للحد الأعلى للفئة الربيعية – التكرار المقابل للحد الأدنى للفئة الربيعية

 

                                        125 – 72

قيمة الربيع الأدنى = 200 + ـــــــــــــــــــــــــ × 100  = 260.227

                                        160 – 72                                              

 

                                                                    ترتيب الربيع الأعلى – التكرار المتجمع للفئة السابقة للفئة الربيعية

قيمة الربيع الأعلى= الحد الأدنى للفئة الربيعية + ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ × طول الفئة      ........ (2)

                                                                                                تكرار الفئة الربيعية *

 

* تكرار الفئة الربيعية = التكرار المقابل للحد الأعلى للفئة الربيعية – التكرار المقابل للحد الأدنى للفئة الربيعية

 

 

                                        375 – 280

قيمة الربيع الأدنى = 400 + ـــــــــــــــــــــــــ × 100  = 463.333

                                        430 – 280                           

نصف المدى الربيعي (الانحراف الربيعي) = ( 463.333 – 260.227 ) ÷ 2 = 203.106 ÷ 2 ≈ 101.5