الربعين (الأدنى والأعلى) والعشيرات والمئينات (أشباه الوسيط)
يفضل الشاشة 1024 ×768
الربيع الأدنى والأعلى(الأول والثالث) Quartiles:
المشاهدات التي نقوم برصدها ضمن مفهوم التكرار في جدول التوزيع التكراري والتي سبق أن حسبنا من خلالها الوسيط والذي يقع ترتيبه في المنتصف (لتكرار) أو التي تكون القيمة التي يقل عنها i50%من المشاهدات ويزيد عنها i50%وبنفس الأسلوب يكون:
يُعرف الربيع الأدنى بالقيمة التي يقل عنها i25%من المشاهدات أو يزيد عنها i75%من المشاهدات ويكون ترتيبه مجموع التكرار مقسوم على أربعة ويحسب كالوسيط.
يُعرف الربيع الأعلى بالقيمة التي يقل عنها i75%من المشاهدات أو يزيد عنها i25%من المشاهدات ويكون ترتيبه مجموع التكرار مضروب في i75%ويحسب كالوسيط.
يرمز للربيع الأول أو الأدنى بالرمز Q1 و يرمز للربيع الثالث أو الأعلى بالرمز Q3 و الوسيط بالرمز Q2 وهو ليس متوسط الربيعين أو لا يساوي ½(Q3 + Q1).
العشيرات ( Deciles ):
مفردها العشير وهو ناتج التقسيم العشري ، i0.1هو العشر الأدنى (D1) من القيم أي ما قبله عشر القيم وبعده تسعة أعشار القيم (i0.9) وتحسب قيمته كحساب الوسيط.
المئينات (Percentile):
المئين الأول هو التقسيم i1من i100ورمزه C1 أي C1 = 0.01 من قيم المعطيات والمئين الستين C60 يقع عند i0.60وتحسب قيمته كحساب الوسيط.
مثال:
الجدول التكراري الآتي يبين بيانات أعمار i30 مريض لمراجعتهم المستشفى والمطلوب حساب الوسيط بكل الطرق الممكنة.
|
الفئات(Interval) |
12 – 14 |
15 – 17 |
18 – 20 |
21 – 23 |
24 – 26 |
27 – 29 |
Total |
|
التكرار(Frequency) |
8 |
4 |
7 |
6 |
2 |
3 |
30 |
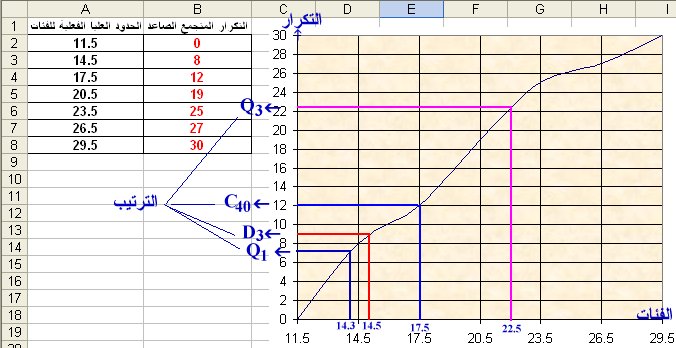
المطلوب حساب كل من Q1 , Q3 , D3 , C40 حسابياً وبيانياً.
الحل:
أولاً: حسابياً:
نكون جدول تكراري المتجمع الصاعد وهو الأساس في حساب المطلوب
| الفئات | الحدود الفعلية للفئات | التكرار | التكرار المتجمع الصاعد |
| 08 – 11 | 11.5 | 0 | 0 |
| 12 – 14 | 14.5 | 8 | 8 |
| 15 – 17 | 17.5 | 4 | 12 |
| 18 – 20 | 20.5 | 7 | 19 |
| 21 – 23 | 23.5 | 6 | 25 |
| 24 – 26 | 26.5 | 2 | 27 |
| 27 – 29 | 29.5 | 3 | 30 |
سنحدد ترتيب كل منهم ثم نعين القيمة بنفس الطريقة التي سبق ذكرها في حساب الوسيط
|
8 ← 3 3 طول الفئة ، i7.5 تقع بين 0 ، 8 (المسافة 8) اللتان تقابل 11.5 ، 14.5 7.5 ← ؟ 7.5 من ( 7.5 – 0 ) ؟ = 3 × 7.5 ÷ 8 = 2.81 ، يضاف لبداية الفئة 11.5 فنحصل على: الربيع الأول Q1 وقيمته = 11.5 + 2.81 = 14.31 |
الترتيب = 30 ÷ 4 = 7.5 |
Q1 |
|
6 ← 3 3 طول الفئة ، 22.5 تقع بين 19 ، 25 (المسافة 6) اللتان تقابل 20.5 ، 23.5 3.5 ← ؟ 3.5 من ( 22.5 – 19 ) ؟ = 3 × 3.5 ÷ 6 = 1.75 ، يضاف لبداية الفئة 20.5 فنحصل على: الربيع الثالث Q3 وقيمته = 20.5 + 1.75 = 22.25 |
الترتيب =3(30 ÷ 4) = 22.5 |
Q3 |
|
4 ← 3 3 طول الفئة ، 9 تقع بين 8 ، 12 (المسافة 4) اللتان تقابل 14.5 ، 17.5 1 ← ؟ 1 من ( 9 – 8 ) ؟ = 3 × 1 ÷ 4 = 0.75 ، يضاف لبداية الفئة 14.5 فنحصل على: الربيع الأول D3 وقيمته = 14.5 + 0.75 = 15.25 |
الترتيب = 3(30 ÷ 10) = 9 |
D3 |
|
القيمة 12 موجودة وتقابل 17.5 أي: C40 = 17.5 |
الترتيب = 40(30 ÷ 100) = 12 |
C40 |
ثانياً: بيانياً:
من برنامج EXCEL نختار رمز Chart Wizard من شريط القوائم ثم Column ← Next ← Rows ← Finish فنحصل على الآتي مع ملاحظة إضافتنا للخطوط الأفقية من نقاط الترتيب للمنحنى والرأسية من نقاط تقاطع الخطوط الأفقية مع المنحنى على المحور الأفقي (الفئات) وكتابة النتائج على المحور الأفقي كما مبين بالشكل الآتي:

المدى الربيعي المتوسط :
هو متوسط الربيعين الأول والثالث أي يساوي نصف مجموعهم وهو يختلف عن Q2 الذي ترتيبه نصف التكرار ويندر استخدامه وخاصة للعينات التي حجمها أكبر من 5.
المدى الربيعي المتوسط = ½(Q3 + Q1) =ـ ½ (i22.5 + 14.31)
= I18.4 " سبق أن حسبنا قيمة الوسيط وكانت I18.8"