مقدمة

التغيرات الدورية والتي سبق ذكرها والمتعلقة بالبيانات السنوية للظاهرة فبالتالي التأثير للتغير الموسمي لا يظهر هنا أي في بيانات السلسلة الزمنية للتغيرات الدورية في حين تتأثر بكل من الاتجاه العام والدورية والعرضية وفي الحالة التي تتكون منها السلسلة ببيانات فصلية لسنوات فيجب إزالة التأثير الموسمي بالإضافة للتأثيرات الأخرى الاتجاه العام والدورية والعرضية ونستخدم نموذج الضرب Y = T × C × I وبقسمة طرفي هذه المعادلة على Ŷ (سبق إيجادها بمعادلة الانحدار) حيث Ŷ = T فنحصل على:

Y ÷ Ŷ = C × I وكنسبة مئوية نقوم بالضرب في 100 للطرفين وهي النسبة الدورية لكون التأثرات العرضية I غير منتظمة فيمكن تجاهلها أي إننا قمنا بفصل عناصر السلسلة الزمنية الثلاثة لنصل للنسب الدورية (Cyclical relatives) كنسب من القيم الاتجاهية ولكوننا نحذف أثر الاتجاه العام فيسميها البعض بالبواقي الدورية النسبية (relative cyclical residuals ) المطلوب حسابها وإن استخدام C × I كتقريب للتغيرات الدورية مقبولاً في السلاسل الزمنية التي بياناتها سنوية ويمكن تحقق ذلك بأحد الطرق الآتية:

1) قسمة قيم السلسلة على قيم الاتجاه العام المقابل لكل منها والناتج يقسم على القياس الموسمي المقابل.

2) قسمة قيم السلسلة على قيمة القياس المسمي المقابل لها والناتج يقسم على قيمة الاتجاه المعني والمقابل لها.

3) ضرب قيمة الاتجاه في قيمة القياس الموسمي المقابل لنحصل على T.S وتعرف بالقيم الطبيعية ونقسم بعدها كل قيمة أصلية على القيمة الطبيعية المقابلة.

كل من هذه الطرق يعتمد على القياس الموسمي والمثال التالي يبين ذلك.

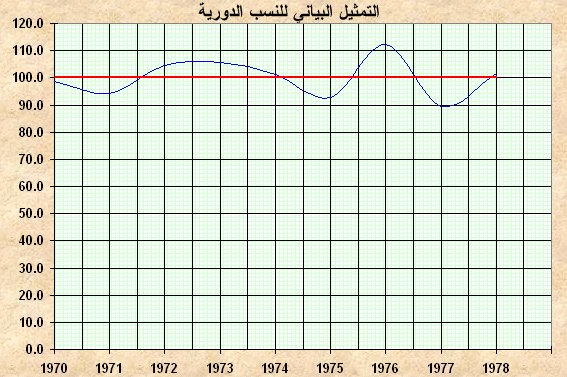
الجدول التالي يبين إنتاج أحد المؤسسات خلال الفترة 1970 ــ 1978 والمطلوب إيجاد كل من خط الاتجاه العام ، والتغيرات الدورية بطريقة النسب الدورية وتمثلها بيانياً

1978	1977	1976	1975	1974	1973	1972	1971	1970	السنة
128	112	140	115	125	130	128	115	120	الإنتاج

نكون جدول شامل للبيانات الخاصة بالمطلوب باعتبار قيم الإنتاج ووضع قيم X المناظرة للسنوات ليكون مجموعها صفر وأخرى لكل من XY k X² وأخرى كما يلي:

( Y ÷ Ŷ ) × 100	Ŷ = 123.67 + 0.53 X	X²	X Y	Y	X	السنة
98.7	121.55	16	– 480	120	– 4	1970
94.2	122.08	9	– 345	115	– 3	1971
104.4	122.61	4	– 256	128	– 2	1972
105.6	123.14	1	– 130	130	– 1	1973
101.1	123.67	0	0	125	0	1974
92.2	124.20	1	115	115	1	1975
112.2	127.73	4	280	140	2	1976
89.4	125.26	9	336	112	3	1977
101.8	125.79	16	512	128	4	1978
		60	32	1113	0	TOTAL

أولاً نوجد خط الاتجاه العام كما سبق ذكر ذلك حال مجموع x يساوي الصفر و بطريقة المربعات الصغرى كما ورد سابقاً في الصيغ:

بالتعويض عن قيم X في المعادلة الاتجاهية Ŷ = 0.53 + 123.67 X نحصل على القيم الاتجاهية الناتجة توضع في عمود Ŷ وسنوجد هنا أحدها ولتكن الأولى:

القيمة الأولى = 123.67 + 0.53 × – 4 = 121.55 ونوجد باقي القيم كما هو مبين في الجدول أعلاه.

نوجد النسب الدورية بالتعويض في الصيغة المبينة في العمود الأخير من الجدول أعلاه وسنوجد هنا أحدها ولتكن الأولى:

القيمة الأولى = (120 ÷ 121.55) × 100 = 0.987 × 100 = 98.7 ونكمل ...

التمثيل البياني للنسب الدورية يبينها الشكل الآتي:

هناك ارتبط قوي بين التغيرات الدورية والحالة الاقتصادية العامة، وتتأثر السلاسل الزمنية بتوقيتها واتساعها فلذا فهي أكثر صعوبة بالتنبؤ بها عنه بالتنبؤ في الاتجاه العام والتغيرات الموسمية.

التنبؤ بالمؤشرات الاقتصادية الخاصة والعامة سواء في حالة الركود أو الانتعاش كالسلسلة الزمنية للإنتاج القومي الإجمالي، ومن السلاسل الزمنية المستخدمة كمؤشر إحصائي للتغيرات الدورية وذات العلاقة بالوضع الاقتصادي فمنها المؤشرات المتقدمة وتتضمن أسعار الأسهم العادية وتصاريح البناء وغيرها وقد تسبق في دورتها التجارية أوجه النشاط العامة في الاقتصاد، والمؤشرات المتزامنة التي تتجه في حركتها لأعلى أو لأسفل مع النشاط الاقتصادي وتتضمن الناتج القومي الإجمالي ومعدل البطالة وتتزامن التحولات الدورية لهذه السلاسل تقريباً مع التحولات الدورية للنشاط الاقتصادي، والمؤشرات المتأخرة كديون البيع والمصروفات الخاصة بالمصانع ويجب استخدام هذه المؤشرات بحرص لعدم انتظامها في توقيتها.

والتنبؤ بالتغيرات الدورية ومن ابسط الطرق إضافة أو إنقاص نسبة معينة من السلسلة باستغلال الفترة السابقة للحالية معتمدين على الوضع الاقتصادي من رواج أو ركود والصعوبة التي تواجه الوضع الاقتصادي من قبل العاملين عليه بعدم الوعي للتغيرات الآتية في الدورة التجارية والتي تسير في الاتجاه المعاكس للوضع الحالي والتوقع في الزيادة بنسبة معينة 5% مثلاً في السنة التالية يعتمد بالضرورة على الذي يمر بفترة الرواج والعكس صحيح فالنقص في المبيعات لشركة ما وبنسبة معينة 5% مثلاُ في حالة مرور النشاط يمر بفترة ركود.