تحليل التباين في اتجاهين
يهدف هذا النوع من التحليل لنوعين من التأثير (أساسي ومشترك) فالتأثير الأساسي للمتغير المستقل يقصد به تأثيره على المتغير التابع بصرف النظر عن مستويات المتغير المستقل الثاني، في حين التأثير المشترك للمتغيرين وهو يعرف أيضاً بالتأثير التفاعلي فهو ناتج عن تفاعل المتغيرين المستقلين ويكون هناك تفاعل بينهم حال اختلاف تأثير أي منهم يختلف باختلاف مستويات الآخر.
لقياس هذا التحليل سنتبع نفس الطريقة في تحليل التباين الأحادي من خلال تقدير التباين في المجتمع بأربع تقديرات معتمدة على أربع مكونات للتباين عبارة عن مجموع المربعات الخاصة بها بتقسيم المجموع الكلي للمربعات إلى كل من تأثير العامل الأول والثاني ـ العاملين ـ (SSB , SSW) والتفاعلي والتباين داخل المجموعات أي المجموع الكلي إلى SSB , SSW ، مجموع المربعات بين المجموعات لكل من مجموع مربعات المتغير المستقل الأول والثاني ومجموع المربعات للتفاعل بين المتغيرين المستقلين والجدول التالي يبين تفاصيل ذلك مع ملاحظة أن SST = SB2 + SW2 , SB2 = SSA + SSB + SSAB
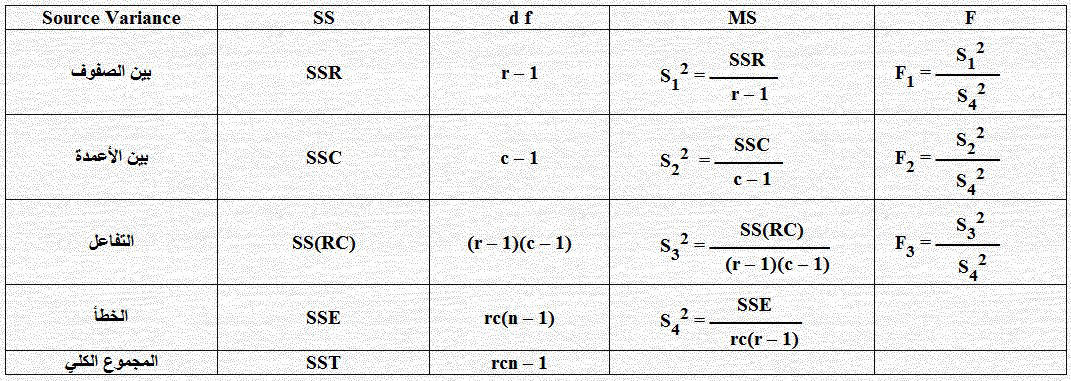
جدول تحليل التباين بمعيارين مع التفاعل الداخلي Two-Ways Analysis of Variance with internal interaction مع عدم وجود تفاعل داخلي
| Source Variance | SS | d f | MS | F |
|
العامل الأول A |
SSA | nA – 1 | MSA | MSA / MSW |
|
العامل الثاني B |
SSB | nB – 1 | MSB | MSB / MSW |
| التفاعل بين المتغيرين | SSAB | (nA – 1)(nB – 1) | MSAB | MSAB / MSW |
| داخل المجموعات | SSW | n – nA nB | MSW | |
| المجموع | SST | n – 1 |
أو:
مجموع مربعات التباين الكلي يتضمن المركبات الأربع التالية وهي مستقلة فيما بينها وتخضع للتوزيع المعتدل بمتوسط صفر وتباين قدره 1 والمركبات الأربع هي:
1) A مركبة بين الأعمدة 2) B مركبة بين الصفوف 3) B, A مركبة التفاعل بين الأعمدة والصفوف 4) eijk مركبة الخطأ حيث أن:
i يشير لعدد الصفوف i = 1 , 2 , 3 , ... , r و r عدد الصفوف
j يشير لعدد الصفوف j = 1 , 2 , 3 , ... , c و c عدد الأعمدة
k يشير لعدد الصفوف k = 1 , 2 , 3 , ... , n و n عدد المشاهدات في الخلية
نستخدم تحليل التباين هذا مع الفرضيات الآتية واستخدام اختبار F:
1) تأثير جميع مستويات العامل A متساوٍ
1) تأثير جميع مستويات العامل B متساوٍ
1) عدم وجود تفاعل بين مستويات العاملين A , B
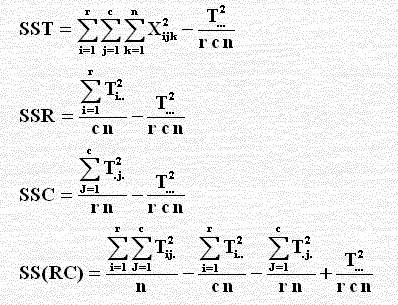
نستخدم الصيغ الآتية لحسابات تحليل التباين الثنائي مع وجود التفاعل الداخلي:

SSE = SST – SSR – SSC – SS(RC)
مع ملاحظة أن:
SST مجموع المربعات الكلي وهو: تربيع كل درجة خام في كل خلية في الجدول ثم نجمع كل المربعات الناتجة (تربيع كل مشاهدة ثم الجمع) ، N عدد الدرجات أو المشاهدات،
ثم نعوض في المعادلة أعلاه للحصول على المطلوب.
SSR مجموع مربعات الصفوف وهو: إن كان لدينا مجموعتان للمقارنة مع ثلاث مستويات مثلاً فلكل مجموعة مقارنة ثلاثة أعمدة(عدد المستويات) لدينا ثلاثة مجاميع للأعمدة
الثلاثة بجمعها نحصل على مجموع الصف للمجموعة الأولى وبالمثل نحصل على مجموع الصف (مجاميع الأعمدة للمجموعة الثانية) وبالتالي يكون لدينا قيمتان مجموع
الصف الأول للممجوعة الأولى ومجموع الصف الثاني للمجموعة الثانية بتربيع كل منهم وجمع المربعين لنحصل على مجموع مربعات الصفوف (راجع القيم المبينة هنا
باللون الأحمر في الجدول هنا مع ملاحظة الجدول هنا لأربع مستويات أي أربع أعمدة في كل مجموعة)، ثم نعوض في المعادلة أعلاه للحصول على المطلوب.
SSC مجموع مربعات الأعمدة لدينا مجموعتان للمقارنة وأربعة مستويات (أنظر الجدول) يعني وجود 4 × 2 = 8 أعمدة أربعة لكل مجموعة وبجمع كل مستوى للمجموعتين
نحصل على مجموع الأعمدة الأربع والمبينة في الجدول بخلفية صفراء اللون في الصف الأخير. فنربع كل منها (4 قيم) ثم نجمع المربعات الناتجة، ثم نعوض في المعادلة
أعلاه للحصول على المطلوب.
SS(RC)i مجموع مربعات الصفوف والأعمدة وهي 8 مجاميع المبينة في الجدول هنا (باللون الوردي) نربع كل منها ونجمع النواتج، ثم نعوض في المعادلة أعلاه للحصول
على المطلوب.
SSE في الجدول هنا 8 مجاميع ( المبينة باللون الوردي) نربع كل منه ونجمع النواتج، ثم نعوض في المعادلة مجموع المربعات الكلي – المجموع الناتج ÷ عدد الدرجات في العمود (للمجموعة الواحدة) هنا يساوي 4 أو من: SSE = SST – SSR – SSC – SS(RC)i
درجات الحرية لتباين الصفوف = عددها – 1
درجات الحرية لتباين الأعمدة = عددها – 1
درجات الحرية لتباين التفاعل = (عدد الصفوف – 1)(عدد الأعمدة – 1)
درجات الحرية لتباين الخطأ = عدد الصفوف × عدد الأعمدة × (عدد درجات المجموعة الواحدة – 1) ، في جدولنا هنا توجد 8 مجاميع كل منها يضم 4 درجات
جدول تحليل التباين:
مثال:
في تقيم لمعرفة تأثير كل من المستوى والفترة الزمنية على أداء الطلاب في مادة الرياضيات فجرى اختيار أربع مستويات أخذ من كل منها 8 طلاب نصفهم للفترة الصباحية والنصف الآخر للفترة المسائية وبصورة عشوائية والمطلوب تحليل التباين ذي اتجاهين لمعرفة الإجابة على التأثير المطلوب حيث كانت نتائجهم في الامتحان النهائي مبينة في الجدول الآتي:
| Time | Levels | |||
| L1 | L2 | L3 | L4 | |
| A M | 60 | 85 | 77 | 80 |
| 75 | 80 | 85 | 85 | |
| 80 | 79 | 67 | 86 | |
| 67 | 66 | 90 | 77 | |
| P M | 90 | 78 | 88 | 85 |
| 90 | 59 | 80 | 66 | |
| 88 | 67 | 78 | 67 | |
| 77 | 85 | 77 | 84 | |
الحل: الحل باستخدام MINITAB حل آخر باستخدام صيغ أخرى
نقوم هنا بإجراء ثلاثة اختبارات وهي التأثير الأساسي للعامل الأول (المستوى) والثاني للفترة الزمنية والثالث للتأثير التفاعلي كما يلي:
1) التأثير الأساسي للعامل الأول (المستوى) نرمز له بالرمز A وفرضيتي العدم والبديل هما:
H0 : μA1=μA2=μA3=μA4 , H1 : على الأقل متوسطين غير متساويين
2) التأثير الأساسي للفترة الزمنية ولنرمز له بالرمز B وفرضيتي العدم والبديل هما:
H0 : μB1=μB2 , H1 : μB1≠μB2
3) التأثير التفاعلي وهو:
H0 : ليس هناك تأثير تفاعلي بين A , B على المتغير التابع
H1 : هناك تأثير تفاعلي بين A , B على المتغير التابع
| Time | Levels | ||||||||
| L1 | L2 | L3 | L4 | Total | LI2 | L22 | L32 | L42 | |
| A M | 60 | 85 | 77 | 80 | 302 | 3600 | 7225 | 5929 | 6400 |
| 75 | 80 | 85 | 85 | 325 | 5625 | 6400 | 7225 | 7225 | |
| 80 | 79 | 67 | 86 | 312 | 6400 | 6241 | 4489 | 7396 | |
| 67 | 66 | 90 | 77 | 300 | 4489 | 4356 | 8100 | 5929 | |
| ∑(AM) | 282 | 310 | 319 | 328 | 1239 | ||||
| P M | 90 | 78 | 88 | 85 | 341 | 8100 | 6084 | 7744 | 7225 |
| 90 | 59 | 80 | 66 | 295 | 8100 | 3481 | 6400 | 4356 | |
| 88 | 67 | 78 | 67 | 300 | 7744 | 4489 | 6084 | 4489 | |
| 77 | 85 | 77 | 84 | 323 | 5929 | 7225 | 5929 | 7056 | |
| ∑(PM) | 345 | 289 | 323 | 302 | 1259 | ||||
| Total | 627 | 599 | 642 | 630 | 2498 | 49987 | 45501 | 51900 | 50076 |
باستخدام الصيغ:

SST = (60)2 + (75)2 + ... + (67)2 + (84)2 – [(2498)2] / [2×4×4]
= 197464 – 195000.13
= 2463.88
SSR = [(1239)2 + (1259)2] / [16] – [(2498)2] / [2×4×4]
= 195012.63 – 195000.13
= 12.50
SSC = [(627)2 + (599)2 + (642)2 + (630)2] / [ 8 ] – [(2498)2] / [2×4×4]
= 195124.250 – 195000.125
= 124.13
SS(RC) = [(282)2 +...+ (302)2] / 4 – 195012.63 – 195124.250 + 195000.13
= 195762 – 195136.75
= 625.25
SSE = SST – SSR – SSC – SS(RC) SSE = 2463.88 – 12.50 – 124.13 – 625.25
= 1702
من جدول f نجد أن:
F1 < f0.05 , 1 , 24 = 4.26 و F2 < f0.05 , 3 , 24 =3.01 و F3 < f0.05 , 3 , 24 = 3.01
جدول تحليل التباين:
| Source Variance | SS | d f | MS | F | F من الجدول |
|
بين الصفوف |
12.50 | 2 – 1 =1 |
S12 = 12.5 / 1 = 12.5 |
F1 = 12.5 ÷ 70.92 = 0.18 |
4.26 |
|
بين الأعمدة |
124.13 | 4– 1 = 3 |
S22 = 124.13 / 3 = 41.4 |
F2 = 41.4 ÷ 70.92 = 0.58 |
3.01 |
| التفاعل | 625.25 | (2 – 1)(4 – 1) = 3 |
S32 = 625.25 / 3 = 208.42 |
F3 = 208.42 ÷ 70.92 = 2.94 |
3.01 |
| الخطأ | 1702.00 | 2×4(4 – 1) = 24 |
S42 = 1702 / 24 = 70.92 |
|
|
| المجموع الكلي | 246388 | 2×4×4 – 1 = 31 |
بناء على قيم F نجد أن:
1) قيمة F المحتسبة أقل من قيم F الجدولية ( 0.18 < 4.26 ) فنقبل فرضية العدم أي عدم وجود اختلاف
2) قيمة F المحتسبة أقل من قيم F الجدولية ( 0.58 < 3.01 ) فنقبل فرضية العدم أي عدم وجود اختلاف
3) قيمة F المحتسبة أقل من قيم F الجدولية ( 2.94 < 3.01 ) فنقبل فرضية العدم أي عدم وجود تفاعل بين العاملين
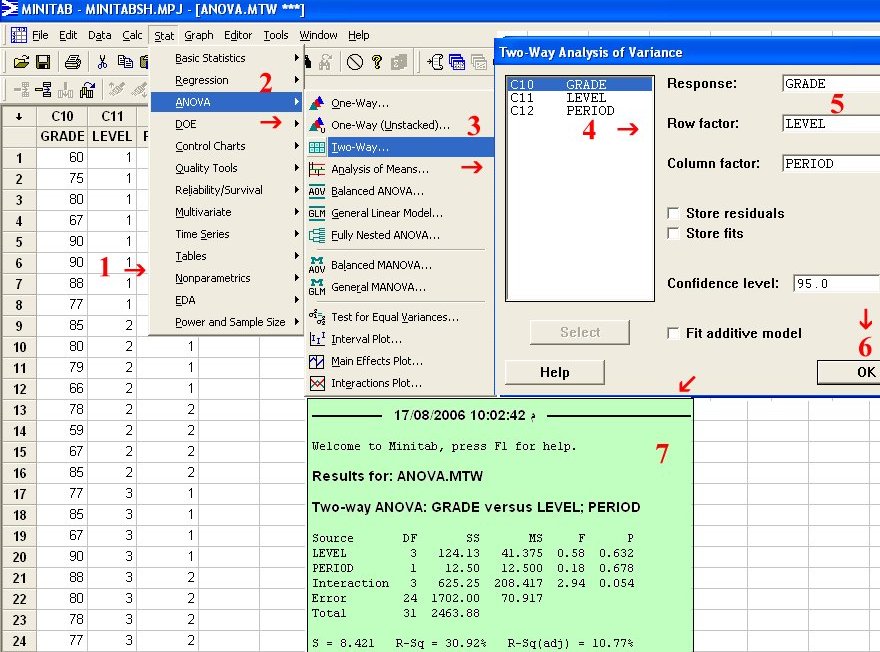
الحل باستخدام برنامج MINITAB للحل كما يلي:
ندخل البيانات في 3 أعمدة، الأول للدرجات في العمود الأول من المستوى الأول إلى الرابع بدء بالدرجات الثمانية للمستوى الأول وللفترتين الصباحية والمسائية
العمود الثاني أمام كل درجة رقم المستوى الخاص بها ولدينا هنا 1 ، 2 ، 3 ، 4
العمود الثالث نعطي الرقم 1 للدرجة الصباحية ، 2 للدرجة المسائية ومن ثم نتبع الخطوات المبينة بالشكل الآتي:
جدول تحليل التباين بمعيارين مع عدم وجود تفاعل داخلي Two-Ways Analysis of Variance without internal interaction
المقصود بعدم وجود تفاعل بين المتغيرين (معياري التصنيف) هو لا يتفاعلان ببقاء تأثير الأعمدة (r) هو نفسه لكل نوع أو صنف والصيغ المستخدمة هنا هي:
والصيغ المستخدمة هي:
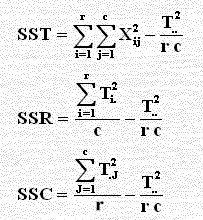
SSE = SST – SSR – SSC
| Source Variance | SS | d f | MS | F |
|
بين الصفوف |
SSR | r – 1 | S12 =SSR / (r – 1) | F1 = S12 / S32 |
|
بين الأعمدة |
SSC | c – 1 | S22 =SSC / (c – 1) | F2 = S22 / S32 |
| الخطأ | SSE | (r – 1)(c – 1) | S32 =SSE / (r – 1)(c – 1) | |
| المجموع | SST | r c – 1 |
مثال:
من أجل تحسين إنتاج مدرس الرياضيات في استخدام العمليات الحسابية قامت أحدى المدارس بإجراء تجربة لمعرفة تأثير ثلاثة طرق من التدريس أ استخدام الآلة الحاسبة ، ب استخدام الحاسب الآلي ، حـ استخدام القوانين وقدمت أربعة أنواع من الحوافز المادي ، المعنوي ، العقاب ، الثواب. اختبر وجود فروق جوهرية بين متوسطات الإنتاج للمدرس وكذلك بين متوسطات الإنتاج واختلاف نوع الحافز عند مستوى معنوية 0.05 من خلال جدول الإنتاج للمدرسين مع الحوافز الآتي:
| الحوافز | الآلة الحاسبة | الحاسب الآلي | القوانين |
| مادي | 60 | 75 | 70 |
| معنوي | 69 | 80 | 60 |
| عقاب | 75 | 77 | 55 |
| ثواب | 58 | 69 | 57 |
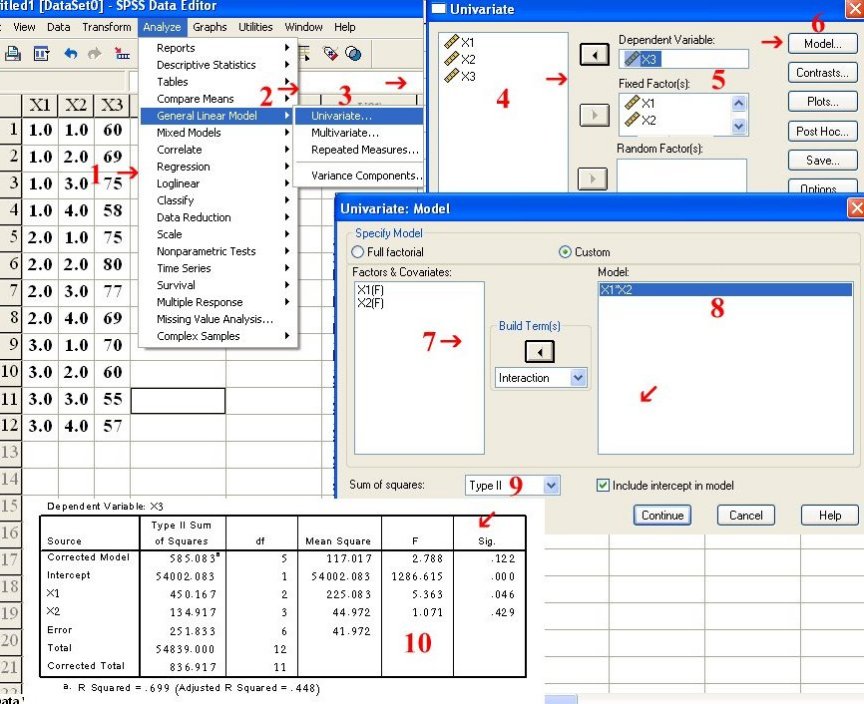
الحل: الحل باستخدام SPSS
نستكمل الجدول بإيجاد مجموع البيانات كالتالي:
| الحوافز | الآلة الحاسبة | الحاسب الآلي | القوانين | Total |
| مادي | 60 | 75 | 70 | 205 |
| معنوي | 69 | 80 | 60 | 209 |
| عقاب | 75 | 77 | 55 | 207 |
| ثواب | 58 | 69 | 57 | 184 |
| Total | 262 | 301 | 242 | 805 |
الفرضيات:
(1) انعدام تأثيرات الصف H0 : a1 = a2 = a3 = a4 = 0
انعدام تأثيرات العمود H0 : b1 = b2 = b3 = 0
(2) على اقل أحداها لا يساوي الصفر : H0
على اقل أحداها لا يساوي الصفر : H1
بتطبيق الصيغ الآتية:
SST = [(60)2 + (69)2 +...+ (55)2 + (57)2] – (805)2 / 4×3
= 54839 – (805)2 / 4×3
= 54839 – 54002.08
= 836.92
SSR = [(205)2 + (209)2 + (207)2 + (184)2] / 3 – (805)2 / 4×3
= 54137 – 54002.08
= 134.92
SSC = [(262)2 + (301)2 + (242)2] / 4 – (805)2 / 4×3
= 54452.25 – 54002.08
= 450.17
SSE = SST – SSR – SSC SSE = 836.92 – 134.92 – 450.17
= 251.83
وجدول تحليل التباين هو:
| Source Variance | SS | d f | MS | F |
|
بين الصفوف |
134.92 | 4 – 1 = 3 | S12 =134.92/ 3 = 44.97 | F1 = 44.97 / 41.97 = 1.071 |
|
بين الأعمدة |
450.17 | 3 – 1 = 2 | S22 =450.17 / 2 = 225.08 | F2 = 225.08 / 41.97 = 5.36 |
| الخطأ | 251.83 | (4 – 1)(3 – 1) = 6 | S32 =251.83 / 6 = 41.97 | |
| المجموع | 836.92 | 4 × 3 – 1 = 11 |
عند مستوى معنوية α = 0.05 نجد أن:
F1 < f0.05 , 3 , 6 = 4.76 قبول الفرضية الصفرية أي لا يوجد اختلاف في متوسط إنتاجية المدرسين عندما تختلف الحوافز
F2 > f0.05 , 2 , 6 = 5.14 عدم قبول الفرضية الصفرية أي يوجد اختلاف في متوسط إنتاجية المدرسين عندما تختلف الحوافز
نتبع الخطوات المبينة بالشكل الآتي: