أجعل حجم الكتابة متوسط لأفضل قراءة التفاضـل
القسم الثالث
قواعد الاشتقاق
أولاً : المشتقة الأولى للمقدار الثابت ص = حـ
البرهان :
ص = د(س) = حـ ← (1)
د(س + هـ) = حـ ← (2) إحداث تغير قدره هـ في س ، لاحظ حـ ثابت لا يحدث أي تغير في قيمتها
ت(هـ) = د(س + هـ) – د(س) = حـ – حـ = 0 بطرح (1) من (2) وهذا قيمة التغير في الدالة
د(س + هـ) – د(س)
م(هـ) = ـــــــــــــــــــــــــــــــــــــــــــ = 0 لاحظ هـ ≠ صفر وهذا قيمة متوسط التغير للدالة وهو
هـ
د(س + هـ) – د(س)
د¯(س) = غــــــــــــــــا ـــــــــــــــــــــــــــــــــــــــــ لاحظ هـ ≠ صفر وهذا قيمة معدل التغير للدالة وهو
هـ ← 0 هـ
= صفر
برهان آخر لمشتقة الثابت
إن الخط البياني للمعادلة ص = حـ هو خط مستقيم يوازي محور السينات فلأي قيمة على الخط البياني س0 ابتدائية ولأي تغير في س فلا يحدث أي تغير مناظر في ص أي أن مقدار التغير ت(هـ) = صفر وبالتالي م(هـ) = 0 وعليه فإن المشتقة الأولى عند س = س0 = صفر أي ص¯ = صفر
فلأي كمية ثابتة تكون المشتقة الأولى صفراً
برهان ثالث لمشتقة الثابت
الدالة ص = حـ يمثلها بيانياً مستقيم يوازي محور السينات و المماس عند أي نقطة هو المستقيم نفسه أي موازياً محور السينات الذي ميله صفر وعليه يكون ميل منحنى الدالة ص = حـ عند أي نقطة عليه = صفر وعليه فالمشتقة الأولى = صفر
المعامل التفاضلي الأول(المشتقة الأولى) للمقدار الثابت = صفر فمثلاً
ص = 7 ¬ ص¯ = صفر
ص = ل ¬ ص¯ = صفر حيث ل ثابت
ثانياً : المشتقة الأولى للدالة ص = د(س) = س تعرف هذه الدالة بالدالة المحايدة
البرهان :
د(س) = س ← (1)
د(س + هـ ) = س + هـ ← (2)
د(س + هـ ) ـ د(س) = هـ وهذا ت(هـ) مقدار التغير في الدالة
د(س + هـ) – د(س) هـ
م(هـ) = ـــــــــــــــــــــــــــــــــــــــــــ = ــــــــ = 1 لاحظ هـ ≠ صفر وهذا قيمة متوسط التغير للدالة وهو
هـ هـ
د(س + هـ) – د(س)
د¯(س) = غــــــــــــــــا ـــــــــــــــــــــــــــــــــــــــــ لاحظ هـ ≠ صفر وهذا قيمة معدل التغير للدالة وهو
هـ ← 0 هـ
= 1
المعامل التفاضلي الأول(المشتقة الأولى) لدالة بالنسبة لنفسها = 1
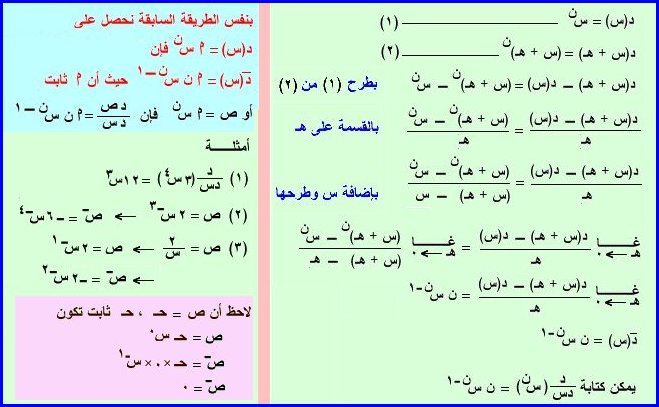
ثالثاً : المشتقة الأولى للدالة د(س) = سن ، د(س) = أ سن الدالة الأسية
البرهان : د(س) = سن

رابعاً : المشتقة الأولى للمجموع الجبري لدالتين أو أكثر
ص = ع ± ى كل من ص ، ع ، ى دوال في المتغير س
ص¯ = ع¯ ± ى¯ يمكن البرهنة بنفس الطريقة السابق
يمكن تعميم ذلك على أكثر من دالتين بالصورة
ص = ع ± ى ± ل كل من ص ، ع ، ى ، ل دوال في المتغير س
ص¯ = ع¯ ± ى¯ ± ل¯ يمكن البرهنة بنفس الطريقة السابق
أمثلـــــــــة
مثال (1)
إذا كان : ص = 3 س4 + 5 س2 – 4 س + 7
فــــإن : ص¯ = 3 × 4 س3 + 5 × 2 س – 4 + 0
ص¯ = 12 س3 + 10 س – 4
مثال آخر (2)
إذا كان : ف = 3 ن2 + 5 ن – 4 ، ف المسافة ، ن الزمن
فـــــإن : ف¯= 6 ن + 5
مثال ثالث (3)
أوجد ميل المماس للمنحنى ص = س3 + 2 س2 – 6 س + 5 عند النقطة ( 1 ، 2 ) وما قيمة الزاوية التي يصنعها هذا الماس مع الاتجاه الموجب لمحور السينات
الحـــل :
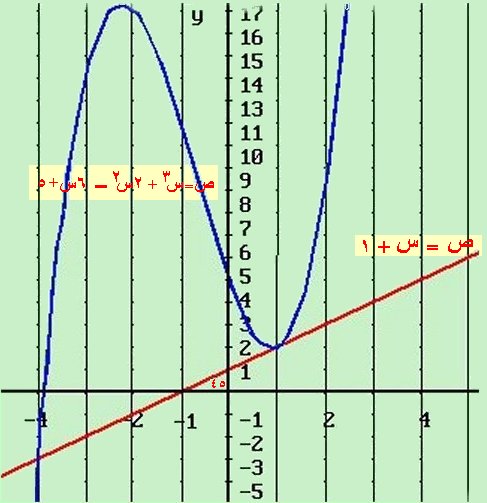
ص = س3 + 2 س2 – 6 س + 5
ص¯ = 3 س2 + 4 س – 6 ميل المماس عند أي نقطة على المنحنى
[ ص¯ ]( 1 ، 2 ) = 3 × 1 + 4× 1 – 6
[ ص¯ ]( 1 ، 2 ) = 1
ميل المماس المطلوب = 1
طـاهـ = 1 حيث هـ الزاوية المطلوبة
هـ = 45ه
خامساً : المشتقة الأولى للدالة ص = ع × ى أو د(س) = ع(س) × ى(س) ـ
البرهان :

أي أن المشتقة الأولى لحاصل ضرب دالتين يساوي الأولى × مشتقة الثانية + الثانية × مشتقة الأولى
مثال :
إذا كانت المشتقة الأولى للدالة حاس هي حتاس فإن
ص = س حاس ص = س حتاس + 1 حاس = س حتاس + حاس
سادساً : المشتقة الأولى لقسمة دالتين ع(س) ، ى(س)

مثل(1) : إذا كانت د(س) = (س + 1)(س3 –4) فأوجد د¯(س)
الحـــل :
د¯(س) = (س + 1) × ( 3س2 –0) + (1 + 0) × (س3 – 4)
د¯(س) = (س + 1) × ( 3س2) + (1) × (س3 – 4)
د¯(س) = 3س2(س + 1) + س3 –4
د¯(س) = 3س3 + 3س2 + س3 –4
د¯(س) = 4س3 + 3س2 –4
يمكن وضع د(س) بصورة كثيرة حدود بالصورة التالية ومن ثم الاشتقاق ويكون هذا حلاً للمسألة كالآتي : ـ
د(س) = س4 + س3 – 4 س –4 ( ناتج ضرب القوسين)
د¯(س) = 4س3 + 3س2 –4 × 1 –0
د¯(س) = 4س3 + 3س2 – 4

سابعاً : المشتقة الأولى لدالة الدالة ص = ع ن
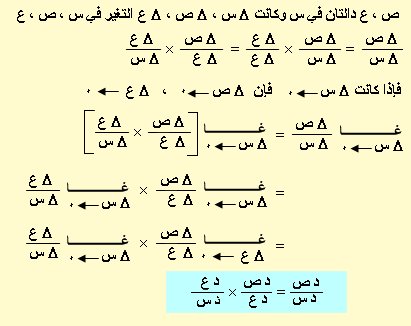
لاحـظ : لا يمكن اختصار د ع مع د ع فليس لها معنى مستقل في حين إمكانيته في D ع ، D ع لوجود معنى لها بقيمة التغير في ع
يمكن وضع القاعدة السابقة على الصورة :ـ ص = ع ن فإن ص¯ = ن ع ن-1 × ع¯
وكثيراً ما نجد الصورة :ـ د(س) = [ ق(س)]ن حيث يكون د¯(س) = ن [ ق(س) ]ن-1 × ق¯(س)
ومن الجدير بالذكر هنا القول بأن ص = س ن يكون ص¯ = ن س ن × 1 حيث 1 مشتقة س كما نعلم وعليه يجب القول دوماً بأن :ـ
مشتقة الدالة الآسية يساوي الأس مضروباً في الدالة بالأس السابق ـ 1 والناتج مضروباً في مشتقة الأساس
مثال (1) :
إذا كانت ص = ( 3 س4 + 2 س –1 )5 فإن
ص¯ = 5( 3 س4 + 2 س –1 )4( 12 س3 + 2 )
ص¯ = 10 (3 س4 + 2 س –1)4 (10 س3 + 1)
وهناك من يعجبه الحل بوضع ع مساوياً ما بداخل القوس ويعوض ويشتق كما يلي : ـ

ثامناً : المشتقة الأولى للدالة الضمنيـة
ما ذا يحدث إذا اشتقينا الدالة ص3 وهي دالة في س ، الأمر بسيط بالقاعدة السابقة 3 ص2 × ص¯ وهذا ما يقودنا للدالة الضمنية وهي الدالة التي تربط المتغيرين س ، ص في صورة معادلة غير محلولة بالنسبة إلى ص كالمعادلة س2 + س ص + ص2 = 5 وبالطبع الدالة ص = ع5 دالة صريحة إذا كانت كل من ع ، ص دوال للمتغير س وسبق اشتقاقها وفي الدوال الضمنية نشتق غالباً بالنسبة للمتغير س كما في المثال التالي
مثال : أوجد قيمة المشتقة الأولى ( ص¯ ) للدالة الضمنية : س2 + ص2 + 6 س – 8 ص – 24 = 0 ( هذه معادلة دائرة )
الحل : س2 + ص2 + 6 س – 8 ص – 24 = 0
2 س + 2 ص ص¯ + 6 – 8 ص¯ = 0 بالقسمة على 2 نحصل على
س + ص ص¯ + 3 – 4 ص¯ = 0
ص ص¯ – 4 ص¯ = – س – 3
ص¯ ( ص – 4 ) = – ( س + 3 ) بالقسمة على – 1
ص¯ ( 4 – ص ) = ( س + 3 )
ص¯ = ( س + 3 ) ÷ ( 4 – ص )