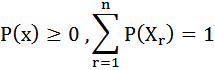
المتغيرات العشوائية Random Variables
المتغير العشوائي المنفصل الوسط للتوزيع الاحتمالي المنفصل التوزيع العشوائي المتصل مثال(2) مثال(3) التباين والانحراف المعياري
المتغير العشوائي:
قد يكون اهتمامنا ليس على عناصر فضاء العينة بل على ربط كل عنصر بقيمة عددية، والقيم العددية هذه ما تعرف بالمتغير العشوائي أي أنًّ:
المتغير العشوائي X هو دالة مجالها مجموعة فضاء العينة ومجالها المقابل مجموعة جزئية R1 من مجموعة الأعداد الحقيقية أي: X: S → R1
ففي تجربة إلقاء قطعة نقود متزنة ثلاث مرات فإن:
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT) N(S) = 8
بفرض أن X هو عدد ظهور H فإن قيم X تأخذ 0 ، 1 ، 2 ، 3 أي عدم ظهور صورة ، صورة ، صورتان ، ثلاث صور أي:
X: S → {0, 1, 2, 3}
ويكون هنا:
P(X=0) = P({TTT}) = 1/8 احتمال عدم ظهور صورة
P(X=1) = P({HTT, THT, TTH}) = 3/8 احتمال عدم ظهور صورة واحدة
P(X=2) = P({HHT, HTH, THH}) = 3/8 احتمال عدم ظهور صورتان
P(X=3) = P({HHH}) = 1/8 احتمال عدم ظهور ثلاث صور
يمكن وضع النواتج في جدول لقيم المتغير العشوائي مع احتمالاتها ويعرف هذا الجدول بالتوزيع احتمالي للمتغير العشوائي X أو على شكل معادلة.
P(x) = P(X = x) = 3Cx × (1/2)3 , 3C0 × 1/8 = 1 × 1/8 = 1/8 (note 3C1 = 3 , 3C2 = 3 , 3C3 = 1) , Table is:
| Xr | 0 | 1 | 2 | 3 | TOTAL |
| P(Xr) |
1 — 8 |
3 — 8 |
3 — 8 |
1 — 8 |
1 |
التوزيعات الاحتمالية المنفصلة Discrete Probability Distributions
المتغير العشوائي المنفصل (Discrete Random Variable)
هو متغير قابلاً للعد ويمكن تمثيله بنقاط منفصلة على خط الأعداد حيث لا توجد أي قيمة بين قيمتين متتاليتين.
التوزيع الاحتماليP(X)i للمتغير العشوائي المنفصل X هو دالة تربط كل عنصر فيه باحتمال العنصر.
حيث احتمال أي عنصر قيمة أكبر من أو يساوي الصفر ومجموع احتمالات العناصر (القيم الممكنة للمتغير) يساوي الواحد الصحيح أي:
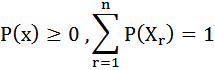
مثال:
عائلة لديها ثلاثة أطفال وعرفنا المتغير العشوائي بعدد الذكور من الأطفال الأربع فأوجد:
1) فضاء العينة.
2) عناصر المتغير العشوائي.
3) التوزيع الاحتمالي.
الحـل:
فضاء العينة هنا هو مجموعة الحالات المختلفة للأطفال الثلاثة من حيث الذكورة والأُنوثة
عناصر المتغير العشوائي هي حالات وجود المطلوب (الذكور هنا) يعني بعدم وجود ذكور أو ذكر واحد أو اثنين أو ثلاثة
N(S) = 23 = 8
1) S = {(B, B, B) , (B, B, G) , (B, G, B) , (G, B, B) , (B, G, G) , ( G, B, G) ,( G, G, B) , (G, G, G)}
2) { 0, 1, 2, 3}
3) X0 = No boys = {(G, G, G)} , N( no boys) = 1 , P(X0) = 1 ÷ 8 = 0.125
X1 = No boys = {(B, G, G) , ( G, B, G) ,( G, G, B)} , N( 1 boys, 2 girls) = 3 , P(X0) = 3 ÷ 8 = 0.375
X2 = No boys = {(B, B, G) , (B, G, B) , (G, B, B)} , N( 2 boys, 1 girl) = 3 , P(X0) = 3 ÷ 8 = 0.375
X3 = No boys = {(B, B, B)} , N( no boys) = 1 , P(X0) = 1 ÷ 8 = 0.125
| Xr | 0 | 1 | 2 | 3 | TOTAL |
| P(Xr) |
1 — = 0.125 8 |
3 — = 0.375 8 |
3 — = 0.375 8 |
1 — = 0.125 8 |
1 |
الوسط للتوزيع الاحتمالي المنفصل:
هو ناتج مجموع حاصل ضرب كل عنصر في احتماله.
ويعرف أيضاً بالقيمة المتوقعة للمتغير العشوائي المنفصل (E(X أو التوقع الرياضي Mathematical Expectation أي أنَّ:
E(X) = (X1) P(X1) + (X2) P(X2) + ... + (Xn) P(Xn)
= ∑ Xi P(Xi) , i = 1, 2, 3, ... , n
وهو يقابل الوسط النظري للمجتمع μ أي: μ = ∑ Xi P(Xi) , i = 1, 2, 3, ... , n
التباين والانحراف المعياري (Variance And Standard Division)
التباين النظري المقابل يكون: σ2 = ∑(Xi – μ)2 P(Xi) , i= 1, 2, 3, ..., n
والانحراف المعياري (Standard deviation) للمتغير العشوائي المنفصل هو الجذر ألتربيعي لقيمة التباين أي σ
بتطبيق ذلك على المثال السابق بإضافة صف جديد نجد أن:
| Xr | 0 | 1 | 2 | 3 | TOTAL |
| P(Xr) |
1 — = 0.125 8 |
3 — = 0.375 8 |
3 — = 0.375 8 |
1 — = 0.125 8 |
1 |
| Xr P(Xr) | 0 | 0.375 | 0.750 | 0.375 |
1.5 |
من العمود الأخير في الجدول نجد أنَّ: μ = 1.5 وهي القيمة المتوقعة ولحساب التباين والانحراف المعياري نطبق العلاقة الرياضية السابقة فنكون الجدول الآتي:
| Xr | P(Xr) | Xr – μ | (Xr – μ)2 | (Xr – μ)2 P(Xr) | X2 P(Xi) |
| 0 |
1 — 8 |
3 – — 2 |
9 — 4 |
9 —— 32 |
0 |
| 1 |
3 — 8 |
1 – — 2 |
1 — 4 |
3 —— 32 |
3 —— 8 |
| 2 |
3 — 8 |
1 — 2 |
1 — 4 |
3 —— 32 |
12 —— 8 |
| 3 |
1 — 8 |
3 — 2 |
9 — 4 |
9 —— 32 |
9 —— 8 |
| TOTAL | 1 | 0 |
24 3 —— = — = 0.75 32 4 |
24 —— = 3 8 |
ومن الجدول والعمود قبل الأخير نجد أن التباين: σ2 = 0.75 والانحراف المعياري 0.8666 (الجذر ألتربيعي للتباين)
يمكن حساب قيمة σ2 من العلاقة : σ2 = ∑X2 P(Xi) – μ2 بإنشاء عمود جديد في الجدول السابق وهو الأخير حيث نجد أنَّ:
σ2 = (3) – (1.5)2
= 0.75
أوجد القيمة المتوقعةE(X)s لمجموع الوجهين الظاهرين في تجربة إلقاء زهرتي النرد مرة واحدة.
الحل:
نكون الجدول التالي للمجموع Xr والاحتمال المقابلP(Xr)s ولحاصل الضربXr P(Xr)s:
| Xr | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | TOTAL |
|
P(Xr) |
1 — 36 |
2 — 36 |
3 — 36 |
4 — 36 |
5 — 36 |
6 — 36 |
5 — 36 |
4 — 36 |
3 — 36 |
2 — 36 |
1 — 36 |
1 |
|
Xr P(Xr) |
2 — 36 |
6 — 36 |
12 — 36 |
20 — 36 |
30 — 36 |
42 — 36 |
40 — 36 |
36 — 36 |
30 — 36 |
22 — 36 |
12 — 36 |
252 —— = 7 36 |
من الجدول والعمود الأخير والصف الأخير تكون القيمة المتوقعة = 7 أي E(X) = 7 أي التوقع الرياضي لمجموع الوجهين الظاهرين = 7
من خواص التوقع الرياضي (Mathematical Expectation):
E(a) = a , a constant
E(aX) = aE(X) , a constant
E(X + Y) = E(X) + E(Y) , X, Y Random variables
E(X × Y) = E(X) × E(Y) , X, Y Independent Random Variables
تقدم 50 طالب لامتحان مادة الإحصاء المشتمل على ستة أسئلة ووزعت نتائج الطلاب حسب عدد الإجابات الصحيحة فكانت كما مبينة في الجدول الآتي:
| TOTAL | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
N(√) |
| 50 | 2 | 4 | 9 | 15 | 10 | 8 | 2 | N (Students) |
أوجد: الوسط (القيمة المتوقعة) باستخدام كل من التوزيع الاحتمالي والتكرار وكذلك التوزيع الاحتمالي مستخدماً التكرار النسبي.
الحل:
لإيجاد الوسط نكون الجدول الآتي:
| TOTAL | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
N(√) -X- |
| 50 | 2 | 4 | 9 | 15 | 10 | 8 | 2 | N (Students) -F- |
| 141 | 12 | 20 | 36 | 45 | 20 | 8 | 0 | X F |
E(X) = 141/50 = 282/100 = 2.82 ≈ 3
لإيجاد الوسط باستخدام التوزيع الاحتمالي نكون الجدول الآتي:
| TOTAL | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
N(√) -X- |
| 50 | 2 | 4 | 9 | 15 | 10 | 8 | 2 | N (Students) -F- |
| i1 | i0.04 | i0.08 | i0.18 | i0.30 | i0.20 | i0.16 | i2÷50 = 0.04 | F% |
| i2.82 | i0.24 | i0.40 | i0.72 | i0.90 | i0.40 | i0.16 | 0 | X F% |
من العمود الأخير والصف الأخير نجد أن:
E(X) = 2.82 ≈ 3
التوزيع الاحتمالي للمتغير العشوائي X هو:
| TOTAL | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
N(√) -X- |
| i1 | i0.04 | i0.08 | i0.18 | i0.30 | i0.20 | i0.16 | i2÷50 = 0.04 | P(X) |
التوزيع العشوائي المتصل(Continuous Random Variable):
يكون X متغير عشوائي متصل إذا أخذ أي قيمة على مجموعة الأعداد الحقيقية أو مجموعة جزئية منها، كالوزن والزمن المستغرق، ...
والتوزيع الاحتمالي المتصل (Continuous Probability Distributions) والذي يعرف بدالة كثافة الاحتمال (متصلة) ويعطي احتمال وقوع قيمة متغير في فترة [a , b] بقيمة المساحة المحصورة بين منحنى دالة الكثافة والمحور السيني والمستقيمان X = a , X = b ودالة الكثافة (التوزيع الاحتمالي) تحقق الآتي:
1) قيمها موجبة F(X) ≥ 0
2) المساحة بين منحناها والمحور السيني = 1
3) المساحة المحصورة بين منحنى دالة الكثافة والمحور السيني والمستقيمان X = a , X = b هيP(a<X<b)s
مثال:
إذا كان التوزيع الاحتمالي لمتغير X له دالة كثافة F(X) = 2/5 – (2/25)X , 0 ≤ X ≤ 5 بين أن هذه الدالة هي دالة كثافة وأوجدP(1 < X < 4)s
الحـل: نرسم منحنى دالة الكثافة في [ 0 ، 5 ] كالآتي:
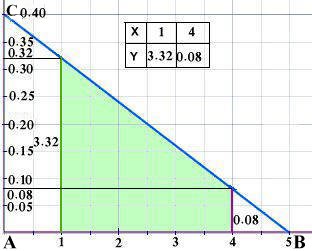
1)المساحة فوق محور السينات فقيم الدالة للمتغير العشوائي موجبة F(X) ≥ 0
|
2) المساحة تحت منحنى الكثافة = مساحة المثلث ABC = 0.5 × 5 × 0.4 = 1 |
Area = Area the triangle ABC = 0.5 × 5 × 0.4 = 1 |
|
3)P(1 < X < 4)s = مساحة شبه المنحرف (اللون الأخضر) = 0.5 ( 0.08 + 3.32 ) × 3 = 5.1 |
P(1 < X < 4) = Green area = 0.5 (0.08 + 3.32) × 3 = 5.1 |