المقدمة:
سبق أن ذكرنا عن دالة توزيع متغير عشوائي منته وتوقعه وأوضحنا ذلك ببعض الأمثلة وهنا نذكر نقاط جديدة وأمثلة جديدة كما يلي:
Examples 1 2 3 4 5 التباين والانحراف المعياري
التوقـع ( E(X) Or μ):
التطبيق ƒ: S →T حيث كل عنصر من T يناظر عنصر من S وتكون ƒ(S)i هي المجال المقابل أو النطاق المصاحب للدالة ƒ وإن التخصيص لعناصر S كمجموع العددين الظاهرين في تجربة
إلقاء حجري نرد يعرف بالمتغير العشوائي، وإذا كان X، Y متغيران عشوائيين على على الفضاء S وإن C عدد ثابت فإنَّ:
" s Î S: (X + Y)(S) = X(S) + X(S) , XY(S) = X(S) Y(S) , (X + C)(S) = X(S) + C , (CX)(S) = CX(S)
دالة الاحتمال:
لتكن X متغير عشوائي معرف على فضاء العينة L حيث أن:
X(L) = { x1, x2, ..., xn}
فتكونX(L)i فضاء احتمال باحتمال xi بأنه P(X = xi)i ويكتب بالصورة ƒ(xi)i وتعرف بدالة احتمال المتغير X أي ƒ(xi) = P(X = xi)i وتكون:
n
ƒ(xi) ≥ 0 , S ƒ(xi) = 1
i =1
تكتب الدالة هذه بصورة الجدول كالآتي:
| xn | ... | x2 | x1 |
| ƒ(xn) | ... | ƒ(x2) | ƒ(x1) |
ويكون التوقع (Expected - Expectation) أو قيمة المتوسط (Average value) أو القيمة المتوقعة للمتغير X ويرمز له E(X)i أو μx اختصاراً μ وتحسب من:
E(X) = x1ƒ(x1) + x2ƒ(x2) + x3ƒ(x3) + ... + xnƒ(xn) = μ
وهو الوسط المرجح(الاحتمالات للدكتور سيمور ليبشتز) للقيم الممكنة للمتغير العشوائي X حيث ترجح القيم لاحتمالها أي كل قيمة بالاحتمال الخاص بها.
n
E(X) = S xiƒ(xi)
i =1
ويلاحظ أنَّ :
E(X2) = x12ƒ(x1) + x22ƒ(x2) + x32ƒ(x3) + ... + xn2ƒ(xn)
n
E(X2) = S xi2ƒ(xi)
i =1
التباين والانحراف المعياري (Variance And Standard Division)
ذكرنا بأن المتغير العشوائي يقيس قيم المتغير X.
ويعرف تباين X ورمزه Var(X)i بما يلي مع العلم بأن E(X) = μ و X المتغير العشوائي له دالة التوزيع المبين في الجدول الآتي:
| xn | ... | x2 | x1 |
| ƒ(xn) | ... | ƒ(x2) | ƒ(x1) |
n
Var(X) = S (xi ─ μ)2 ƒ(xi) = E((X ─ μ)2)
i =1
ويعرف الانحراف المعياري بأنه الجذر ألتربيعي للتباين ويرمز له بالرمز σx ويمكن وضع الصيغة التالية لحساب التباين:
Var(X) = E(x)2 ─ μ2
The prove
n n
S xiƒ(xi) = 1 , S ƒ(xi) = μ ........ (1)
i =1 i =1
n
Var(X) = S (xi ─ μ)2 ƒ(xi)
i =1
n
Var(X) = S (xi2 ─ 2μxi + μ2)ƒ(xi) فك القوس
i =1
n n n
Var(X) = S xi2ƒ(xi) ─ 2μS xiƒ(xi) + μ2Sƒ(xi) إدخال السجما
i =1 i =1 i =1
n
Var(X) = S xi2ƒ(xi) ─ 2μ μ + μ2 1 التعويض من المعادلات في (1) أعلاه
i =1
n
Var(X) = S xi2ƒ(xi) ─ 2μ2 + μ2 التعويض من المعادلات في (1) أعلاه
i =1
n
Var(X) = S xi2ƒ(xi) ─ μ2 المطلوب
i =1
Or
n
Var(X) = S E(X2) ─ [E(X)]2
i =1
ألقي حجري نرد مرة واحدة ولتكن X تخصص لكل زوج من فضاء النواتج القيمة الأصغر لعنصري الزوج المرتب. احسب توقع X والتباين والانحراف المعياري.
الحــل:
فضاء النواتج S حيث:
S = {(1, 1), (1, 2), ... , (6, 6)}
X متغير عشوائي لكون أن:
X(a, b) = a if a < b Or b if b < a
وعليه تكون النتائج لكافة الأزواج هي القيم من الواحد الصحيح حتى الستة وتكون X متغير عشوائي أي أن:
X(S) = {1, 2, 3, 4, 5, 6}
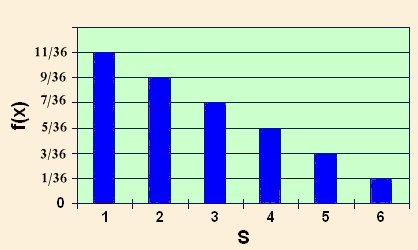
والتوزيع الاحتمالي ƒ للمتغير العشوائي X يحسب كالتالي :
مع ملاحظة أنَّ ƒ(1) = C حيث C احتمال الأزواج التي يكون فيها العدد الأصغر يساوي i1
11
ƒ(1) = P(X = 1) = P({(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (3, 1), (4, 1),(5, 1), (6, 1)} = —
36
9
ƒ(2) = P(X = 2) = P({(2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 2), (4, 2), (5, 2), (6, 2)} = —
36
7
ƒ(3) = P(X = 3) = P({(3, 3),(3, 4), (3, 5), (3, 6), (4, 3), (5, 3), (6, 3)} = —
36
5
ƒ(4) = P(X = 4) = P({(4, 4),(4, 5),(4, 6), (5, 4), (6, 4)} = —
36
3
ƒ(5) = P(X = 5) = P({(5, 5), (5, 6), (6, 5)} = —
36
1
ƒ(6) = P(X = 6) = P({(6, 6)} = —
36
يمكن وضع هذه النتائج في جدول كالآتي:
| 6 | 5 | 4 | 3 | 2 |
1 |
xi |
|
1 — 36 |
3 — 36 |
5 — 36 |
7 — 36 |
9 — 36 |
11 — 36 |
ƒ(xi) |
نعلم أنَّ:
E(X) = x1ƒ(x1) + x2ƒ(x2) + x3ƒ(x3) + ... + xnƒ(xn)
بالإمكان إضافة صف جديد للجدول السابق يبين الطرف الأيسر في E(X)i كالتالي:
| 6 | 5 | 4 | 3 | 2 |
1 |
xi |
|
1 — 36 |
3 — 36 |
5 — 36 |
7 — 36 |
9 — 36 |
11 — 36 |
ƒ(xi) |
|
6 — 36 |
15 — 36 |
20 — 36 |
21 — 36 |
18 — 36 |
11 — 36 |
xiƒ(xi) |
11 + 18 + 21 + 20 + 15 + 6 91
E(X) = —————————— = — ≈ 2.5
36 36
Expected Value = 2.5
نضيف صف جديد للجدول السابق xi2ƒ(xi)i لحساب التباين والانحراف المعياري كالتالي:
| 6 | 5 | 4 | 3 | 2 |
1 |
xi |
|
1 — 36 |
3 — 36 |
5 — 36 |
7 — 36 |
9 — 36 |
11 — 36 |
ƒ(xi) |
|
6 — 36 |
15 — 36 |
20 — 36 |
21 — 36 |
18 — 36 |
11 — 36 |
xiƒ(xi) |
|
36 — 36 |
75 — 36 |
80 — 36 |
63 — 36 |
36 — 36 |
11 — 36 |
xi2ƒ(xi) |
11 + 36 + 63 + 80 + 75 + 36 301
E(X2) = —————————— = — ≈ 8.4
36 36
n
Var(X) = S E(X2) ─ [E(X)]2
i =1
= 8.4 ─ (2.5)2
= 2.15
——
σ = √ 2.15 = 1.466
لاحظ المستطيلات الرأسية هي احتمالات قيم عناصرS.

تمرين: في المثال السابق لتكن X تُخصص للزوج (a, b) القيمة الأصغر. (الجواب i(7)
صُممت قطعة نقود بحيث يكون احتمال ظهور الصورة i3/4 واحتمال ظهور الكتابة i1/4 فألقيت ثلاث مراث. أكتب فضاء النواتج، وأحسب توقيع المتغير المتغير العشوائي X الذي يخصص لكل نقطة من فضاء النواتج أكبر عدد لمرات ظهور الصورة وكذلك التباين والانحراف المعياري.
الحــل:
P(H) = 3/4 احتمال ظهور الصورة
P(T) = 1/4 احتمال ظهور الكتابة
S = {HHH, HHT, HTH, THH, TTH, THT, HTT, TTT}
نحسب احتمالات عناصر الفضاء الثمانية كالآتي:
P(HHH) = 3/4×3/4×3/4 = 27/64 ظهور ثلاث صور
P(HHT) = 3/4×3/4×1/4 = 0.141 , P(HTH) = 3/4×1/4×3/4 = 9/64 , P(THH) = 1/4×3/4×3/4 = 9/64 ظهور صورتان وكتابة
P(TTH) = 1/4×1/4×3/4 = 3/64 , P(THT) = 1/4×3/4×1/4 =3/64 , P(HTT) = 3/4×1/4×1/4 =3/64 ظهور كتابتان وصورة
P(TTT) = 1/4×1/4×1/4 = 1/64 ظهور ثلاث كتابات
نحسب النطاق المصاحب (المجال المقابل) للمتغير العشوائي X كالآتي:
X(HHH) = 3 عدد الصور
X(HHT) = X(HTH) = X(THH) = 2 عدد الصور
X(TTH) = X(THT) = X(HTT) = 1 عدد الصور
X(TTT) = 0 عدد الصور
X(S) = { 0, 1, 2, 3} المجال المقابل
نحسب الاحتمالات المقابلة كالآتي:
ƒ(0) = P(TTT) = 1/64 عدم ظهور صورة
ƒ(1) = P(HTH U THT U TTH U HTT) = 9/64 + 3/64 + 3/64 + 3/64 = 18/64 ظهور صورة منفردة
ƒ(2) = P(HHT U THH) = 9/64 + 9/64 = 18/64 ظهور صورتان على التوالي
ƒ(3) = P(HHH) = 27/64 ظهور ثلاث صور على التوالي
يمكن وضع النواتج في جدول كالآتي:
| Total | 3 | 2 | 1 |
0 |
xi |
|
64 — = 1 64 |
27 — 64 |
18 — 64 |
18 — 64 |
1 — 64 |
ƒ(xi) |
نضيف صف جديد للجدول السابق يبين حاصل ضرب xiƒ(xi)i كالآتي:
| Total | 3 | 2 | 1 |
0 |
xi |
|
64 — = 1 64 |
27 — 64 |
18 — 64 |
18 — 64 |
1 — 64 |
ƒ(xi) |
|
135 —— = 2.11 64 |
81 — 64 |
36 — 64 |
18 — 64 |
0 |
xiƒ(xi) |
E(X) = 2.11
نضيف صف جديد للجدول السابق xi2ƒ(xi)i لحساب التباين والانحراف المعياري كالتالي:
| Total | 3 | 2 | 1 |
0 |
xi |
|
64 — = 1 64 |
27 — 64 |
18 — 64 |
18 — 64 |
1 — 64 |
ƒ(xi) |
|
135 —— = 2.11 64 |
81 — 64 |
36 — 64 |
18 — 64 |
0 |
xiƒ(xi) |
|
333 —— = 9.25 36 |
243 —— 36 |
72 — 36 |
18 — 36 |
0 |
xi2ƒ(xi) |
0 + 18 + 72 +243 333
E(X2) = ——————— = —— ≈ 9.25
36 36
n
Var(X) = S E(X2) ─ [E(X)]2 التباين
i =1
= 9.25 ─ (2.11)2
= 4.8
——
σ = √ 4.8 = 2.2 الانحراف المعياري
تمرين: في المثال السابق إذا صُممت القطعة بحيث الاحتمال للصورة i 5 ÷3 وللكتابة i5 ÷ 2أوجد التوقع الرياضي. (الجواب: i1.66)
صندوق يحوي i20 لمبة كهرباء من بينها i4 لمبات تالفة (معيبة). سحبت من الصندوق i4 لمبات، أوجد القيمة المتوقعة لعدد اللمبات المعيبة والتباين والانحراف المعياري.
الحــل:
المعيب من اللمبات قد يكون: i 4 or 3 or 2 or 1 or 0
فضاء العينة S وعدد كل منه كالتالي:
20C4 = 4845 عدد الوحدات السليمة والمعيبة
16C4 × 4C0 = 1820 × 1 = 1820 الوحدات الأربع سليمة
16C3 × 4C1 = 560 × 4 = 2240 ثلاثة وحدات سليمة وواحدة معيبة
16C2 × 4C2 = 120 × 6 = 720 وحدتان سليمة ووحدتان معيبة
16C1 × 4C3 = 16 × 4 = 64 وحدة واحدة سليمة وثلاث وحدات معيبة
16C0 × 4C4 = 1 × 1 = 1 الوحدات الأربع معيبة
يمكن وضع النواتج (للوحدات المعيبة) في جدول كالآتي:
| Total | 4 | 3 | 2 | 1 |
0 |
xi |
|
4845 —— = 1 4845 |
1 —— 4845 |
64 —— 4845 |
720 —— 220 |
2240 —— 4845 |
1820 —— 4845 |
ƒ(xi) |
نضيف صف جديد للجدول السابق يبين حاصل ضرب xiƒ(xi)i كالآتي:
| Total | 4 | 3 | 2 | 1 |
0 |
xi |
|
4845 —— = 1 4845 |
1 —— 4845 |
64 —— 4845 |
720 —— 220 |
2240 —— 4845 |
1820 —— 4845 |
ƒ(xi) |
|
3876 —— = 0.8 4845 |
4 —— 4845 |
192 —— 4845 |
1440 —— 4845 |
2240 —— 4845 |
0 |
xiƒ(xi) |
E(X) = 0.8
نضيف صف جديد للجدول السابق xi2ƒ(xi)i لحساب التباين والانحراف المعياري كالتالي:
| Total | 4 | 3 | 2 | 1 |
0 |
xi |
|
4845 —— = 1 4845 |
1 —— 4845 |
64 —— 4845 |
720 —— 220 |
2240 —— 4845 |
1820 —— 4845 |
ƒ(xi) |
|
3876 —— = 0.8 4845 |
4 —— 4845 |
192 —— 4845 |
1440 —— 4845 |
2240 —— 4845 |
0 |
xiƒ(xi) |
|
5712 —— = 1.2 4845 |
16 —— 4845 |
576 —— 4845 |
2880 —— 4845 |
2240 —— 4845 |
0 |
xi2ƒ(xi) |
0 + 2440 + 2880 + 576 + 16 5712
E(X2) = ——————————— = —— ≈ 1.2
4845 4845
n
Var(X) = S E(X2) ─ [E(X)]2 التباين
i =1
= 1.2 ─ (0.8)2
= 0.56
——
σ = √0.56 = 0.75 الانحراف المعياري
قيل لشخص بأن يلقي حجر النرد فله من الدنانير لكل عدد زوجي وعليه من الدنانير لكل عدد فردي. هل هذه العينة ملائمة للشخص ليكسب.
الحــل:
الجدول الآتي يبين النتائج لحساب التوقع علماً بأن القيمة السالبة تعني الخسارة وهي للأعداد الفردية:
| Total | ─ 3 | ─ 2 | ─ 1 | 6 | 4 |
2 |
xi |
|
64 — = 1 6 |
1 — 6 |
1 — 6 |
1 — 6 |
1 — 6 |
1 — 6 |
1 — 6 |
ƒ(xi) |
|
6 — = 1 6 |
─ 3 —— 6 |
─ 2 —— 6 |
─ 1 —— 6 |
6 — 6 |
4 — 6 |
2 — 6 |
xiƒ(xi) |
E(X) = 1
من حيث أنَّ القيمة المتوقعة موجبة فاللعبة ملائمة للشخص للكسب.
تمرين: قيل لشخص بأن يلقي حجر النرد فله من الدنانير لكل عدد فردي وعليه من الدنانير لكل عدد زوجي. هل هذه العينة ملائمة للشخص ليكسب. (الجواب: اللعبة غير ملائمة للشخص للكسب)
ألقيَّ حجري نرد وليكن X متغير عشوائي يعين مجموع العددين الظاهرين على حجري الترد احسب كل من التوقع ، التباين ، الانحراف المعياري.
الحــل:
أقل مجموع للوجهين الظاهرين هو i2 من الزوج ( i1، 1) وأكبر مجموع هو i12 من الزوج ( i6، 6) ونكون الجدول للنتائج كما يلي:
| 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 |
2 |
xi |
|
1 — 36 |
2 — 36 |
3 — 36 |
4 — 36 |
5 — 36 |
6 — 36 |
5 — 36 |
4 — 36 |
3 — 36 |
2 — 36 |
1 — 36 |
ƒ(xi) |
لاحظ أن: البسط في الصف الثاني يمثل عدد الأزواج للمجموع المقابل له في الصف الأول كما هو مبين باللون الأصفر فمثلاً العدد i7 في الصف الأول يتأتي من جمع العنصرين في سبعة أزواج أي:
7 → (1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)
| Total | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 |
2 |
xi |
|
36 — = 1 36 |
1 — 36 |
2 — 36 |
3 — 36 |
4 — 36 |
5 — 36 |
6 — 36 |
5 — 36 |
4 — 36 |
3 — 36 |
2 — 36 |
1 — 36 |
ƒ(xi) |
|
252 —— = 7 36 |
12 — 36 |
22 — 36 |
30 — 36 |
36 — 36 |
40 — 36 |
42 — 36 |
30 — 36 |
20 — 36 |
12 — 36 |
6 — 36 |
2 — 36 |
xi ƒ(xi) |
|
1974 —— = 54.8 36 |
144 — 36 |
242 — 36 |
300 — 36 |
324 — 36 |
320 — 36 |
294 — 36 |
180 — 36 |
100 — 36 |
48 — 36 |
18 — 36 |
4 — 36 |
xi2 ƒ(xi) |
——
Expected = μx = E(X) = 7 , Var(X) = E(X2) ─ E(X)2 = 54.8 ─ 49 = 5.8 , SD = σ = √ 5.8 = 2.4