(1) أذكر مميزات الوسيط
أ) عدم تأثره بالقيم الشاذة.
ب) تعتمد قيمته على التكرارات.
ج) يوجد في كل البيانات التي تتصف بالترتيب
(2) أذكر عيوب الوسيط
ا) يهتم بالقيم الوسطى للبيانات فقط
ب) لا يصلح لإعطاء فكرة عن النزعة المركزية للبيانات في فئات متباعدة
ج) لا يسهل التعامل معه في التحاليل الإحصائية في دراسة ظاهرة ما في عدة عينات.
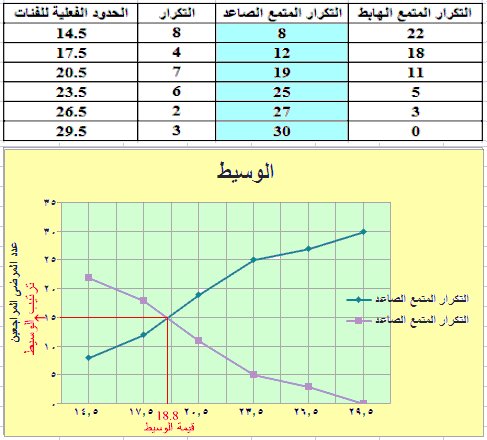
(3) كيف يحسب الوسيط بيانياً؟
أ) تكوين جدول تكراري متجمع صاعد أو هابط أو كلاهما
ب) نحسب ترتيب الوسيط ويساوي نصف مجموع التكرار
ج) نحدد قيمة الترتيب على محور التكرار
د) نرسم خط أفقي من قيمة الترتيب (الواقعة على محور التكرار) ليلاقى المنحنى الصاعد أو النازل في نقطة ( في المنحنيين النازل والصاعد هي نقطة تقاطعهم)
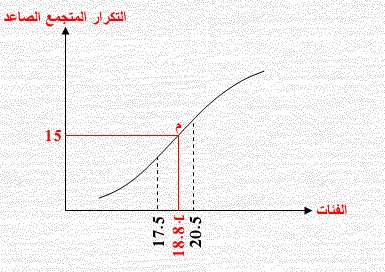
هـ) من النقطة على المنحنى نسقط عموداً على الخط الأفقي (الفئات) والقيمة هنا هي قيمة الوسيط.

الشكل التالي يوضح ذلك
(4) وضح بأمثلة مدى تأثر الوسيط بالعمليات الحسابية
لتكن لدينا القيم i 5 ، 8 ، 12 ، 9 ، 10 ، 15 ، 17 والمطلوب الوسيط
نرتب القيم تصاعدياً تنازلياً (تنازلياً مثلاً) أي i 5 ، 8 ، 9 ، 10 ، 12 ، 15 ، 17 فالوسيط هو i10
لنقم بالعمليات الحسابية الأربع على البيانات الأصلية بعد ترتيبه تنازلياً كما مبين بالجدول الآتي:
| العملية الحسابية | البيانات | الوسيط | ملاحظات | ||||
|
الجمع: لنضف العدد i3 للمفردات (بعد الترتيب) |
8, 11, 12, 13, 15, 18, 20 |
13 |
الوسيط الجديد = الوسيط السابق + i3 |
||||
|
الطرح: لننقص العدد i4 من كل مفردة |
1, 4, 5, 6, 8, 11, 13 |
6 |
الوسيط الجديد = الوسيط السابق – i4 |
||||
|
الضرب: نضرب كل مفردة في i3 |
15, 24, 27, 30, 36, 45, 51 |
30 |
الوسيط الجديد = الوسيط السابق × i3 |
||||
|
القسمة:: نقسم كل مفردة على العدد i2 |
2.5, 4, 4.5, 5, 6, 7.5, 8.5 |
5 |
الوسيط الجديد = الوسيط السابق ÷ ii2 |
بناء ما ورد في الجدول يتأثر الوسيط بالعمليات الحسابية الأربع وإن أجريت أكثر من عملية فمثلاً إذا أضفنا العددi2 على كل مفردة ثم ضربنا النواتج في i3 فالوسيط الجديد للبيانات بعد الإضافة والضرب( i21, 30, 33, 36, 42, 51, 57) يكون مضافاً للوسيط السابق i2 ومضروباً في i3 أي i(10 +2) × 3 = 36
(5) إذا كان الوسيط للقيم i3 ، 6 ، 4، 7، 1، X هو K فما قيمة الوسيط للقيم i5 ، 8 ، 6، 9 ، 3 ، X + 2 بدلالة K
يلاحظ أن القيم الجديدة هي القيم السابقة بعد إضافة العدد i2 لكل قيمة فالوسيط الجديد = i2 + K
(6) أضغط هنا