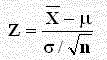
الاختبار الأحادي

الاستدلال عن متوسط مجتمع                   الاستدلال عن النسبة في المجتمع                     اختبار تباين مجتمع

    يهدف الاختبار لمعرفة وجود فرق جوهري بين متوسط العينة ومتوسط المجتمع ويشمل حالة معلومة تباين المجتمع ، مجهولة التباين

حالة معلومة تباين المجتمع σ² ( معلومية الانحراف المعياري)

    وهي الحالة التي نعتبر فيها فرضية العدم بتساوي متوسطي العينة والمجتمع في مقابل عدم تساويهم للفرضية البديلة حيث أن:

(1) المجتمع طبيعي أو حجم العينة كبير

(2) المعلمة محل الاختبار هي متوسط المجتمع μ

(3) تقدير النقطة للمعلمة هو متوسط العينة X`

                         ـــــ

(3) الخطأ المعياري SE = σ ÷ Ö n

(4) حساب قيمة Z من الصيغة الرياضية التالية ومقارنتها مع مع Z الجدولية عند مستوى المعنوية المطلوب.

استخدم جدول Z بالضغط هنا            استخدم جدول T بالضغط هنا

مثال (1):

    أجرى اختبار شفوي لتحديد مستوى i25 طالب في العمليات الحسابية فيما كان المتوسط يقل عن i30 درجة فكانت نتائج الطلاب هي:

i23    33    37    38    34    29    24    26    37    31    35    40    20   24    35    37       

أختبر الفرضية (المتوسط  يساوي i30 أو يختلف عنه ) باعتبار أن البيانات تتبع توزيع طبيعي بانحراف معياري i5 وعند مستوى معنوية i5%

الحــل:

    H₀ : m = 30الفرضية الصفرية  

الفرضية البديلة      H₁ : m ¹ 30

بحساب الوسط الحسابي نجده i 512 ÷ 16 = 32

بتطبيق الصيغة الرياضية السابقة لحساب Z

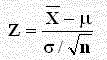
     32 – 30

= ــــــــــــــــــ   

  i   5 / 4

=i1.60

<i1.96

 لا يمكن رفض الفرضية الصفرية بمعنى عدم وجود اختلاف جوهري بين متوسط العينة ومتوسط المجتمع

مثال آخر:

    اختيرت عينة مكونة من i 64 فطيرة من مطعم وكان متوسط  الوزن له اi 60 جرام بانحراف معياري i 5 ويزعم صاحب المطعم أن متوسطه وزن الفطيرة التي يبيعها i 62 جرام. بين إن كان قول صاحب المطعم مقبول عند مستوى معنوية 1%

الحـــل:

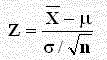
     i62 – 60

= ــــــــــــــــــ   

     i5 / 8

=i3.2

>i2.58

نرفض قول صاحب المطعم بمستوى معنوية i1%

حالة عدم معلومة تباين المجتمع σ² ( عدم معلومية الانحراف المعياري)

    وهي الحالة الغالبة حيث نأخذ التقدير من نتائج العينة وباستخدام الإحصاءة T بدلاً من Z مع درجات حرية n – 1 وتكون الصيغة الرياضية المستخدمة هي:

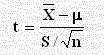
مثال:

    أخذت عينة عشوائية لأربع وحدات i36 ، 45 ، 50 ، 81 من مجتمع طبيعي باعتقاد أن متوسطه i70 وانحرافه المعياري غير معروف. هل متوسط العينة يختلف معنوياً عن متوسط المجتمع بمستوى معنوية i5%؟

الحـــل:

الحــل:

    H₀ : m = 70الفرضية الصفرية  

الفرضية البديلة       H₁ : m ¹ 70

الاختبار ذو جانبين ( عدم التساوي) ، درجات الحرية i3 ويكون:

t_{0.05/2, 3} = 3.182

بحساب الوسط الحسابي نجده:  i( 36 + 45 + 50 + 81 ) ÷ 4 = 53

وبحساب S من القانون:

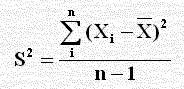
          = [ (36 – 53)² + (45 – 53)² +(50 – 53)² +(81 – 53)² ] / 3

          = [ 289 + 64 + 9 + 784 ] / 3

          = 382

       S = 19.55

بتطبيق الصيغة الرياضية السابقة لحساب Z

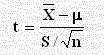
       = ( 53 – 70 ) ÷i( 19.55 / 2 )

       = – 1.74

ومن حيث قيمة t المحتسبة أقل من i3.181 أو أكبر من i – 3.182 فلا داعي لرفض الفرضية الصفرية ونقبل بعدم وجود فرق معنوي بين متوسطي المجتمع والعينة.

الحل باستخدام SPSS

مثال:

     أخذت عينة عشوائية مكونة من i100 مراجع لمستشفى ما واستفسر منهم عن عدد المراجعات للمستشفى خلال السنتين الماضيتين فتبن أن المتوسط هو i6 بانحراف معياري i3.5 في حين أن إدارة المستشفى تدعي بأن مراجعة كل شخص لا تقل في المتوسط عن i5 مراجعات خلال نفس الفترة المذكورة عند مستوى معنوية i1%.

بين مدى صحة ادعاء إدارة المستشفى.

الفرضية هنا من جانب واحد وهي:

    H₀ : m ³ 5الفرضية الصفرية  

الفرضية البديلة       H₁ : m < 5

قيمة Z من الجدول عند i0.01 هي i2.32 وبتطبيق الصيغة الرياضية التالية لحساب Z

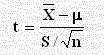
      = ( 6 – 5 ) / ( 3.5/10)

      = 10 / 3.5

      = 2.88

وحيث أن قيمة Z المحسوبة ( i2.88 ) أكبر من قيمة Z الجدولية فنرفض إدعاء إدارة المستشفى.