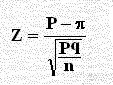
نستخدم هنا اختبار Z أو اختبار χ2 للظواهر التي لا يمكن قياسها ولكن يمكن تقدير نسبة وقوعها كنسبة الأميين في المجتمع أو نسبة الحاصلين على شهادة الماجستير
والرمز P يعطى لنسبة الوقوع (النجاح) ويكون P – 1 نسبة عدم الوقوع (الفشل) ويرمز له بالرمز q ويرمز للنسبة المتوقعة بالرمز π ونستخدم الصيغة التالية:
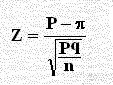
مثال:
تدعى إحدى الشركات بأن مالا يقل عن 92% من إنتاجها مطابق للمواصفات وللتحقق من ذلك أخذنا عينة عشوائية من إنتاج الشركة حجمها 81 وحدة إنتاجية وتبين بعد الفحص أن 90% مطابق للمواصفات. هل هذه النتيجة مطابقة لادعاء الشركة عند مستوى معنوية 5%؟
الحـــل:
| الفرضية الصفرية |
H0 : m ³ 0.92 |
| الفرضية البديلة |
H1 : m < 0.92 |
من الجدول عند مستوى معنوية 5% نجد أن Z0.05 = 1.64 ( نبحث في الجدول عن المساحة 0.9500 أو أقرب قيمة لها (0.9505 يقابلها 1.65 لقيمة Z )
بافتراض أن خاصية النسبة مقارب للتوزيع الطبيعي حيث أن حجم العينة أكبر من 30
نطبق
الصيغة الرياضية السابقة :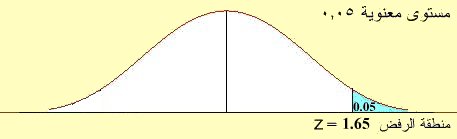
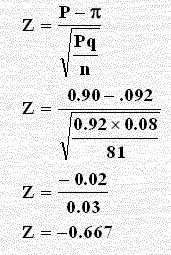
وقيمة Z المحتسبة أقل من قيمة Z الجدولية فنقبل ادعاء الشركة عند مستوى معنوية 5%.
يمكن حل المثال السابق باستخدام χ2 من القانون:
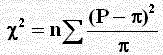
حيث P النسبة الملاحظة ، π النسبة المتوقعة ولحل المثال السابق
| الفرضية الصفرية |
H0 : m ³ 0.92 |
| الفرضية البديلة |
H1 : m < 0.92 |
من الجدول عند مستوى معنوية 5% نجد أن Z0.05 = 1.64 ( نبحث في الجدول عن المساحة 0.9500 أو أقرب قيمة لها (0.9505 يقابلها 1.65 لقيمة Z )
بافتراض أن خاصية النسبة مقارب للتوزيع الطبيعي حيث أن حجم العينة أكبر من 30
نطبق الصيغة الرياضية السابقة :
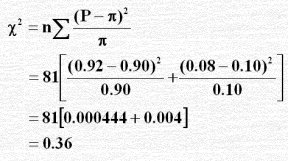
وقيمة Z المحتسبة أقل من قيمة Z الجدولية فنقبل ادعاء الشركة عند مستوى معنوية 5%.