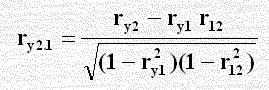
معامل الارتباط الجزئي:
هذا المعامل يقيس الارتباط بين أي زوج من المتغيرات عند ثبات المتغيرات الأخرى ويرمز له بالرمز r12. 345 فالارتباط هنا بين المتغيرين X1 , X2 وثبات الثلاثة الأخرى X3 , X4 , X5 ويستخدم لتحديد العلاقة بين متغيرين محددين أو للتعرف على متغيرات يراد حذفها بسبب عدم تأثيرها على المتغير التابع ومربع معامل الارتباط الجزئي يعرف بمعامل التحديد الجزئي، ويجب ملاحظة أن ry1 رمز للعلاقة بين y , x1 في حين ry1. 2 رمز للعلاقة بين y , x1 مع ثبات x2. يحسب معامل الارتباط الجزئي من الصيغة الرياضية الآتية ( بين y , x2 وثبات x1 ):
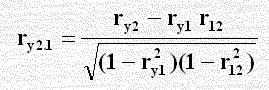
يلاحظ أن قيمة r سبق ذكرها ونعيدها هنا للتذكير(في أول الصفحة)
مثال:
أوجد معامل الارتباط الجزئي للمثال الوارد في معامل الارتباط المتعدد وهو:
أرادت مؤسسة للدعاية والإعلان معرفة العلاقة بين عدد المستجيبين لإعلاناتها y وحجم الإعلان المنشور في الصحيفة X1 وعدد الصحف الموزعة X2 التي تنشر الإعلان وحصلت المؤسسة على البيانات التالية:
عدد المستجيبين بالمئات ( yi ) ، حجم الإعلان بالإنش (X1 ) ، عدد الصحف الموزعة بالآلف (X2)
الحل:
حصلنا على النتائج: ry1 = 0.909 , ry2 = 0.731 , r12 = 0.741 في المثال المذكور
بتطبيق الصيغة الرياضية أعلاه لحساب معامل الارتباط الجزئي ry2.1
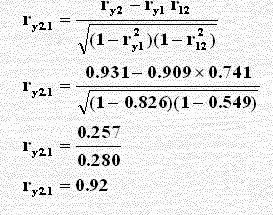
إن قيمة معامل الارتباط الجزئي 0.92 تؤدي لمساهمة عالية ( معامل التحديد الجزئي = 0.85 ) في تفسير تباين y وبمكن اختبار فرضية العدم بالاحصاءة t من أن معامل الارتباط الجزئي للمجتمع P تساوي صفر أي Ho : Py1.2... k ونحسب t من الصيغة التالية
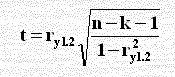
مع درجات حرية n – k – 1 = 6 – 3 – 1 = 2 ومقارنة t الناتجة بـ t الجدولية عند مستوى معنوية α = 0.05.
ويكون الاختبار:
Ho : Py1.2 = 0 و H1 : Py1.2 ≠ 0 ومن الجدول نجد أن: t 0.025 , 2 = 4.303
وبالتعويض:
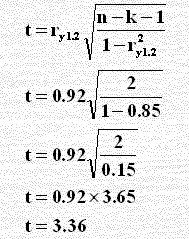
وحيث أن قيم t = 3.36 أقل من من قيمة t = 4.303 الجدولية فنقبل فرض العدم ويعني عدم معنوية معامل الارتباط الجزئي للمجتمع المتغير Py2.1 X1 .