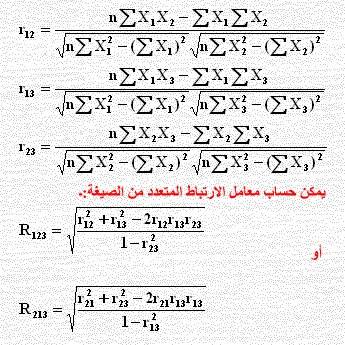
معامل الارتباط المتعدد:
هذا المعامل والذي يرمز له بالرمز R أيضاً يقيس قوة العلاقة بين أكثر من متغيرين وهي مغيرات عشوائية متصلة التوزيع (توزيع متعدد المتغيرات Multivariate distribution) وإن حساب قيمة R هو امتداد لقيمة معامل الارتباط البسيط (r) مع استبدال X ,Y بـ X1–Xk , Y ولنأخذ ثلاث متغيرات X1, X2, X3 نحصل على الصيغ الآتية:
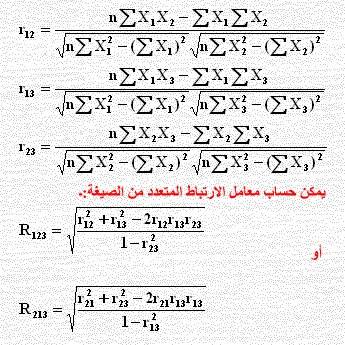
ومعامل الارتباط المتعدد قيمته بين الصفر والواحد الصحيح وهو موجب دائماً
مثال:
أرادت مؤسسة للدعاية والإعلان معرفة العلاقة بين عدد المستجيبين لإعلاناتها y وحجم الإعلان المنشور في الصحيفة X1 وعدد الصحف الموزعة X2 التي تنشر الإعلان وحصلت المؤسسة على البيانات التالية:
عدد المستجيبين بالمئات ( yi ) ، حجم الإعلان بالإنش (X1 ) ، عدد الصحف الموزعة بالآلف (X2)
|
X2 |
X22 |
X1 |
X12 |
yi |
yi2 |
yiX1 |
yiX2 |
X1X2 |
|
2 |
4 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
|
8 |
64 |
8 |
64 |
4 |
16 |
32 |
32 |
64 |
|
1 |
1 |
3 |
9 |
1 |
1 |
3 |
1 |
3 |
|
7 |
49 |
5 |
25 |
3 |
9 |
15 |
21 |
35 |
|
4 |
16 |
6 |
36 |
2 |
4 |
12 |
8 |
24 |
|
6 |
36 |
10 |
100 |
4 |
16 |
40 |
24 |
60 |
|
28 |
170 |
33 |
235 |
15 |
47 |
103 |
88 |
188 |

اختبار فرضية العدم Ho : Py.12...k = 0 نحسب F من الصيغة:
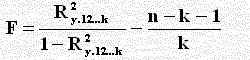
حيث k عدد المتغيرات ونقارن قيمة F المحسوبة من الصيغة الرياضية السابقة مع قيمة F الجدولية فإن كانت أقل نقبل Ho
من الجدول نجد أن F 0.025,3,2 = 16.04 ومن الصيغة أعلاه نجد أن:
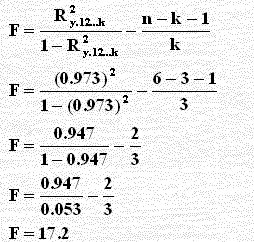
وبما أن 17.2 > 16.04 فنرفض الفرضية الصفرية ونستدل على معنوية R