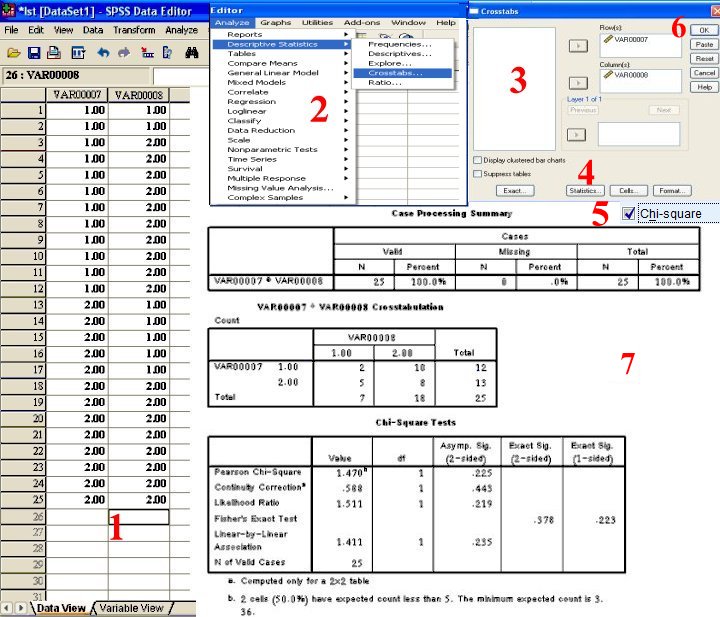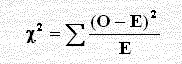
معامل ( χ2 )
يقرأ كآي تربيع ويستخدم للبيانات المعبر عنها بالتكرار في مستويين أو أكثر كالذكور والإناث أو مدينة ، وقرية ، منطقة وهدفه حساب معامل الارتباط لنسبتين أو أكثر لمتغير واحد ( أحادي) أو متغيرين تصنيفين يضم كل منهم مستويين أو أكثر (ثنائي).
وصيغته الرياضية هي:
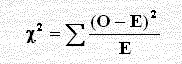
حيث O التكرار الملاحظ ، E التكرار المتوقع ويساوي (حاصل ضرب المجموع الأفقي للتكرار للخلية × المجموع الرأسي للتكرار) ÷ ( المجموع الكلي للتكرار) ونبين ذلك بالمثال التالي: مثال آخر
| أنثى | ذكر | المجموع | |
| يدخن | 2 | 10 | 12 |
| لا يدخن | 5 | 8 | 13 |
| المجموع | 7 | 18 | 25 |
سنعدل في الجدول لإضافة E ونرمز للتكرار O فيصبح الجدول كالآتي:
| أنثى | ذكر | المجموع | |||
| يدخن | O = 2 | E = 7 × 12 ÷ 25 = 3.36 | O = 10 | E = 18 × 12 ÷ 25 = 8.64 | 12 |
| لا يدخن | O = 5 | E = 7 × 13 ÷ 25 = 3.64 | O = 8 | E = 18 × 13 ÷ 25 = 9.36 | 13 |
| المجموع | 7 | 18 | 25 | ||
وعليه يمكن حساب χ2 كالآتي بعد تبسيط الجدول السابق:
|
أنثى |
ذكر |
||
|
O = 2 |
E = 3.36 |
O = 10 |
E = 8.64 |
|
O = 5 |
E = 3.64 |
O = 8 |
E = 9.36 |
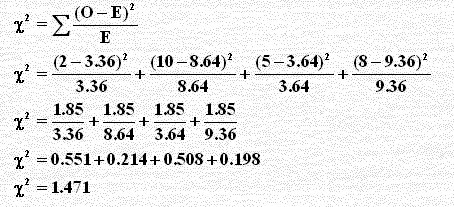
1- نقارنها مع القيمة الجدولية بدرجة حرية 1 [من (عدد الصفوف - 1)(عدد العمدة - 1)] عند مستوى معنوية 0.05 مثلاً : فنجدها في الجدول 3.841 وذلك بهدف اتخاذ القرار
2- بقسمة χ2 = 1.471 على n = 25 حجم العينة يكون الناتج 0.0588 وبأخذ الجذر التربيعي 0.243 وهو معامل فاي (راجع العلاقة بين فاي وكآي تربيع).
وباستخدام برنامج SPSS ولصغر حجم العينة ندخل البيانات في عمودين الأول يمثل العدد 1 لتكرارات الصف الأول أي 2 ، 10 أي ندخل العدد 1 أثنتا عشرة مرة وندخل 2 للصف الثاني 13 مرة
(5 + 8) وندخل في العمود الثاني العدد 1 مرتين للعدد 2 , 2 عشر مرات للعدد 10 ثم ندخل العدد 1 خمسة مرات للعدد 5 والعدد 2 ثماني مرة للعدد 8 كما مبين في الشكل التالي. هنا طريقة أخرى باستخدام SPSS