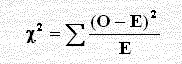
مثال: لاحظ الحل باستخدام البرنامج الإحصائي SPSS أسفل الصفحة حل آخر باستخدام البرنامج الإحصائي SPSS
الجدول التالي يبين مشاهدات 150 مربية أطفال حسب مستواهم العلمي في اللعب الإيهامي للأطفال والمطلوب قياس مدى اختلاف التكرارات المشاهدة والتكرارات المتوقعة عند مستوى معنوية 0.01
( α=0.01 ) باستخدام معامل كا2( χ2 ) حسابياً وتحقق من ذلك باستخدام البرنامج الإحصائي SPSS
| المستوى التعليمي | الملاحظة | المجموع | ||||
| كثيراً جداً | كثيراً | متوسط | قليلاً | قليلاً جداً | ||
| شهادة الثانوية أو ما يعادلها | 25 | 17 | 11 | 4 | 3 | 60 |
| دبلوم سنتين بعد الثانوية | 22 | 15 | 7 | 2 | 2 | 48 |
| الشهادة الجامعية | 21 | 12 | 6 | 3 | 0 | 42 |
| المجموع | 68 | 44 | 24 | 9 | 5 | 150 |
الفرضية الصفرية H0 : يوجد تجانس للمشاهدات
الفرضية البديلة H1 : عدم وجود تجانس للمشاهدات
مستوى المعنوية α = 0.01
درجات الحرية = (3 - 1) × (5 - 1) = 2 × 4 = 8
من جدول χ2 من صف 8 وعمود 0.01 تكون χ2 0.01,8= 20.090 لاحظ عند مستوى معنوية 0.05 يكون: χ2 0.05,8= 15.507
نكون جدول التكرارات المتوقعة لقيم التكرارات الملاحظة (المشاهدات) حيث:
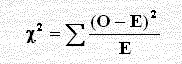
حيث O التكرار الملاحظ ، E التكرار المتوقع ويساوي (حاصل ضرب المجموع الأفقي للتكرار للخلية × المجموع الرأسي للتكرار) ÷ ( المجموع الكلي للتكرار) وجدول القيم المتوقعة E للقيم الملاحظة هو:
| المستوى التعليمي | الملاحظة | ||||
| كثيراً جداً | كثيراً | متوسط | قليلاً | قليلاً جداً | |
| شهادة الثانوية أو ما يعادلها | 27.20 | 17.60 | 9.60 | 3.60 | 2.00 |
| دبلوم سنتين بعد الثانوية | 21.76 | 14.08 | 7.68 | 2.88 | 1.60 |
| الشهادة الجامعية | 19.04 | 12.32 | 6.72 | 2.52 | 1.40 |
نكون جدولاً جديداً بحساب (القيم الملاحظة - القيمة المتوقعة)2 ÷ القيمة المتوقعة كالآتي:
| المستوى التعليمي | الملاحظة | |||||
| كثيراً جداً | كثيراً | متوسط | قليلاً | قليلاً جداً | المجموع | |
| شهادة الثانوية أو ما يعادلها | 0.178 | 0.020 | 0.204 | 0.044 | 0.500 | 0.947 |
| دبلوم سنتين بعد الثانوية | 0.003 | 0.060 | 0.060 | 0.269 | 0.100 | 0.492 |
| الشهادة الجامعية | 0.202 | 0.008 | 0.077 | 0.091 | 1.400 | 1.779 |
| المجموع | 0.382 | 0.089 | 0.342 | 0.405 | 2.000 | 3.218 |
من الجدول نجد أن: χ2 0.01,8 = 20.090 أكبر من χ2 = 3.218 المحسوبة لاحظ يمكن استخدام القانون في المثال السابق لحساب χ2
حيث أن القيمة الجدولية أكبر من القيمة المحسوبة والتي تقع ضمن منطقة القبول لذا نرفض الفرضية البديلة ونؤكد بوجود تجانس للمشاهدات.
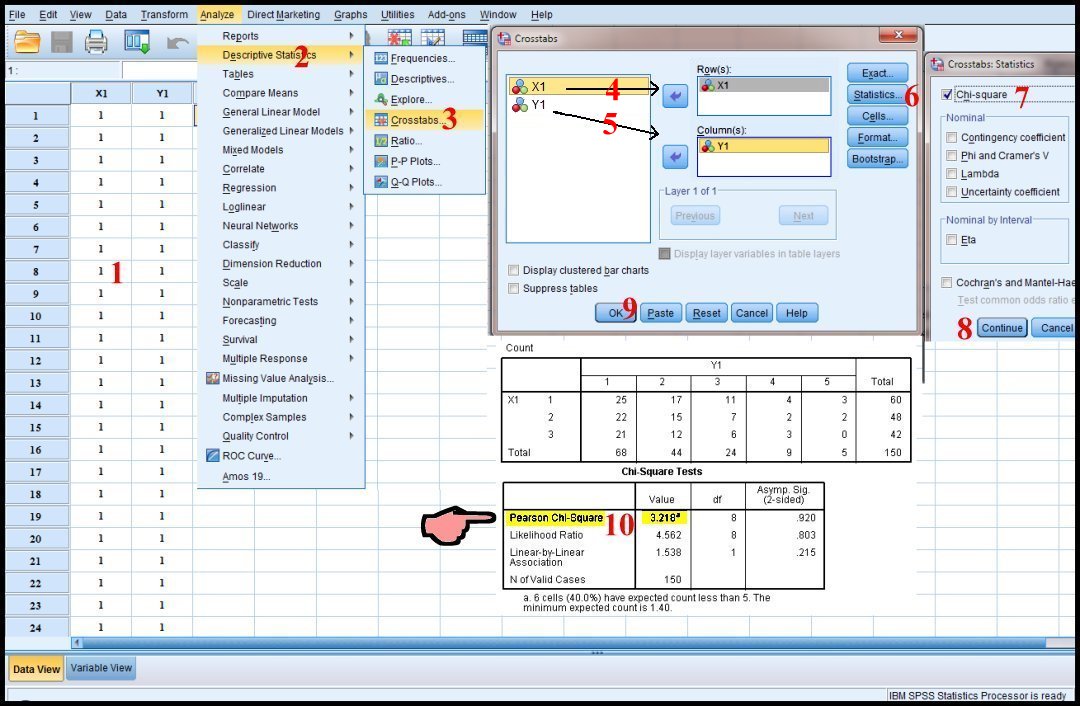
وباستخدام برنامج SPSS ندخل البيانات في عمودين الأول يمثل العدد 1
لمجموع تكرارات الصف الأول أي ندخل العدد 1 ستون مرة وندخل 2 لمجموع الصف الثاني وندخل 3 لمجموع الصف الثالث وفي العمود الثاني ندخل العدد 1 مكرر 25 مرة والعدد 2 مكرر 17 مرة والعدد 3 مكرر 11 مرة والعدد 4 مكرر 4 مرات والعدد 5 مكرر 3 مرة ثم ندخل العدد 1 مكرر 22 مرة والعدد 2 مكرر 15 مرة والعدد 3 مكرر 7 مرات والعدد 4 مكرر 2 مرة والعدد 5 مكرر 2 مرة ثم ندخل العدد 1 مكرر 21 مرة والعدد 2 مكرر 12 مرة والعدد 3 مكرر 6 مرة والعدد 4 مكرر 3 مرات والعدد 5 مكرر 0 مرة ونحسب χ2 كما سبق - لاحظ الشكل التالي - هنا حل آخر باستخدام الكلمة للبيانات بدل الأعداد