|
|
يفضل استخدام الخط حجم المتوسط أو الكبير View, Text size, medium or Larger لاحظ الشكل
|
|
التكاملات القياسية العامة
1) ∫ ( س + ب)ن د س
من حساب المشتقة الأولى:
د
ـــــــــ ( س + ب)ن + 1 = ( ن + 1 )( س + ب)ن × 1 = ( ن + 1 )( س + ب)ن
د س
1 د
وبالنقل والترتيب نحصل على : ( س + ب)ن = ــــــــــــــ × ـــــــــ ( س + ب)ن + 1
ن + 1 د س
د 1
أي أن : ( س + ب)ن = ــــــــــ [ ـــــــــــــــ ( س + ب)ن + 1]
د س ن + 1
( س + ب )ن + 1
أي أن : ∫ ( س + ب)ن د س = ــــــــــــــــــــــــــــــ + ث
ن + 1
القانون صحيح لجميع قيم ن عدا القيمة ن = –1 وواضح أن الأس ن + 1 يصبح –1 + 1 = صفر مقسوماً على الصفر فيعطي كمية غير معينة وهذا
يقودنا للقول بأن اللوغاريتم للدالة لوهـ ( س + ب ) مشتقته الأولى هي 1 ÷ ( س + ب ) أي (س + ب)–1 وعليه يكون :
∫ ( س + ب)–1 د س = لوهـ ( س + ب ) + ث
في حال وجود ثابت كمعامل للمتغير س أي حـ س حيث حـ الثابت فنقسم على هذا الثابت في ناتج التكامل والإثبات بنفس الطريقة السابقة فنحصل على :
(حـ س + ب )ن + 1
أي أن : ∫ (حـ س + ب)ن د س = ـــــــــــــــــــــــــــــــــ + ث
حـ( ن + 1)
1
∫ ( حـ س + ب)–1 د س = ـــــ لوهـ (حـ س + ب ) + ث
حـ
أمثلة :
( 5 + 2س )3 + 1
مثال(1) ∫ ( 5 + 2س)3 د س = ــــــــــــــــــــــــــــــــ + ث
2 × (3 + 1)
( 5 + 2س )4
= ــــــــــــــــــــــــــــــــ + ث
2 × 4
1
= ــــ ( 5 + 2س )4 + ث
8
1 1
مثال(2) ∫ ـــــــــــــــــــــ د س = ـــــ لوهـ (2 س + 3 ) + ث
2 س + 3 2
1 1
مثال(3) ∫ ـــــــــــــــــــــ د س = – ـــ لوهـ (2 س + 3 ) + ث
3 –2 س 2
1
مثال(4) ∫ ـــــــــــــــــــــ د س = ∫ (3س +5)–5 د س
(3س +5)5
(3س +5)–5+1
= ــــــــــــــــــــــــــــــ + ث
3 × (–5 + 1)
1
= – ــــــ (3س +5)–4 + ث
12
1
= – ــــــــــــــــــــــــــــــ + ث
12(3س +5)4
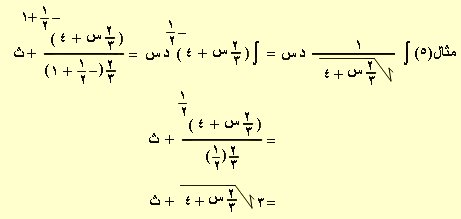
مما سبق يمكن وضع تصور عام لتكامل دالة أسية (كحد واحد) بزيادة الأس واحد والقسمة على الأس الجديد وفي حالة وجود معامل س نقسم عليه أما أن تكون الدالة الأسية بحدين بالصورة (أ س + ب) أيضاً نضيف للأس واحد ونقسم على أ مضروباً في الأس الجديد ، ويمكن قول ذلك بطريق أخرى حيث نعلم أن مشتقة الدالة الأسية هو الأس مضروباً في الدالة بعد إنقاص أسها 1 ثم نضرب في مشتقة الأساس نوضح ذلك بالمثال :
مشتقة حان س هو ن × حان–1 س × حتاس × 1 حيث 1 مشتقة س أي نشتق الزاوية أيضاً مثل
( حا4(3س) )/ = 4 × حا3(3س) × حتا3س × 3 ... الضرب في الأس × الدالة بأس ناقص 1 × مشتقة الأساس × مشتقة الزاوية وهذا يقودنا للقول:
تكامل الدالة الأسية يوجب توفر مشتقة أساسها للحصول على ناتج هو نفس الدالة الأسية بزيادة أسها واحد والقسمة على الأس الجديد أي أنَّ :
ق[د(س])ن+1
∫ ق[د(س)]ن د/(س) د س = ــــــــــــــــــــــــ + ث
ن + 1
فمثلاً :
(2س3 + 3 س + 4)5
(1) ∫ (2س3 + 3 س + 4)4 (6س2 + 3) د س = ــــــــــــــــــــــــــــــــــــ + ث لاحظ القوس الثاني مشتقة الأساس(داخل القوس الأول).
5
حا5س
(2) ∫ حا4س حتاس د س = ـــــــــــــ + ث لاحظ أن حتاس مشتقة جاس
5
–12حتا4(6س) 1
(3) ∫ 12حتا3(6س) حا(6س) د س = ـــــــــــــــــــــــــــــــ + ث = – ــــ حتا4(6س) + ث لاحظ أن مشتقة حتاس هي – جاس
6 × 4 2
سنورد جدول التكاملات القياسية أعم من الجدول الوارد سابقاً(في المقدمة) مع ملاحظة عدم قبول بعضه في المرحلة الثانوية كحل للمسائل وسنوضح ذلك لاحقاً في حينه
1 (أ س + ب)ن+1
(1) ∫ (أ س + ب)ن د س = ــــ ــــــــــــــــــــــــــــ + ث ، ن ≠ – 1
أ ن + 1
1 1
(2) ∫ حا(أ س + ب) د س = – ــــ حتا(أ س + ب) + ث (3) ∫ حتا(أ س + ب) د س = ــــ حا(أ س + ب) + ث
أ أ
1 1
(4) ∫ قا2(أ س + ب) د س = ــــ طا(أ س + ب) + ث (5) ∫ قتا2(أ س + ب) د س = – ـــ طتا(أ س + ب) + ث
أ أ
1 1
(6) ∫ قا(أ س + ب) طا(أ س + ب) د س = ــــ قا(أ س + ب) + ث (7) ∫ قتا(أ س + ب) طتا(أ س + ب) د س = – ــ قتا(أ س + ب)+ ث
أ أ
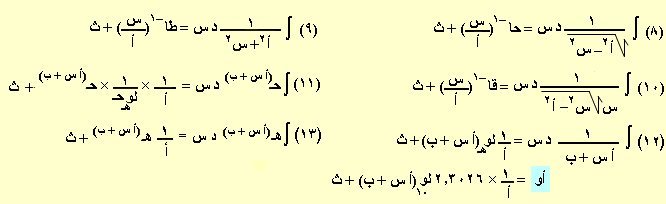
مثال(1) : احسب ∫ حا(3 + 4 س) د س
الحــل :
1
∫ حا(3 + 4 س) د س = – ــــ حتا(3 + 4 س) + ث
4
مثال(2): أوجد تكامل 6هـ2س بالنسبة إلى س
الحــل :
1
∫ 6هـ2س د س = 6 × ـــ هـ2س + ث
2
= 3 هـ2س + ث
مثال(3): أوجد تكامل 6×(2)2س+5 بالنسبة إلى س تمـاريـن
الحــل :
1 1
∫ 6×(2)2س+5 د س = 6 × ـــ × ـــــــــــ × (2)2س+5 + ث
2 لوهـ2
3
∫ 6×(2)2س+5 د س = ـــــــــــ × (2)2س+5 + ث
لوهـ2