يفضل استخدام الخط حجم المتوسط من View, Text size, medium  لاحظ الشكل في اليسار

                       التكامل     

مقدمـة : ـ

    التكامل وبكل بساطة هو عملية عكسية للتفاضل وبالتالي أصعب من التفاضل كما هو متعارف عليه بأن العمليات العكسية أصعب كالقسمة والضرب والتربيع وإيجاد الجذر التربيعي، ومن المفيد أيضاً معرفتنا المسبقة بكل قواعد التفاضل والتحليل وحساب المثلثات وما إلى ذلك من القوانين التي سيكون لها الأثر الفعال في التكامل، فإذا فرضنا أن ع مشتقة ص بالنسبة إلى س أي ع = ص¯ تستعمل عندما تكون ص معلومة والمطلوب إيجاد مشتقتها الأولى ع ، وبصورة أخرى نقول أن ع . د س هو تفاضل ص بالنسبة إلى س أي ع . د س = د ص تستعمل إذا كانت ع معلومة والمطلوب تكامل تكاملها(ص) فبالتعريف  نقول تكامل الدالة ع بالنسبة إلى س هو الدالة التي مشتقتها الأولى بالنسبة إلى س هي ع أو التي تفاضلها بالنسبة إلى س هي ع . د س فيكون الدالة ص تكامل الدالة ع بالنسبة إلى س ونكتب ذلك بالصورة ص = ∫ ع . د س حيث ∫ رمز التكامل وهو غالباً من تكبير حرف S من كلمة Sum التي تعني الجمع حيث سنبين ذلك لاحقاً بأن التكامل لدالة هو المسحة تحت منحنى الدالة والتي تحسب بمجموع المستطيلات كما أن د س تدل على التفاضل وأمثلة ذلك :

ص = س³     فإن     ع = ص¯ = 3 س²     فنقول     ص = ∫ ع . د س =  ∫3 س² . د س = س³ 

ص = 2س³ + 3 س   فإن   ع = ص¯ = 6 س² + 3    فنقول     ص = ∫ ع . د س =  ∫(6 س² + 3) . د س = 2س³ + 3 س

ص = حاس     فإن     ع = ص¯ = حتا س     فنقول      ص = ∫ ع . د س =  ∫ حتا س . د س =  حا س

ص = حتاس     فإن     ع = ص¯ = – حا س     فنقول    ص = ∫ ع . د س =  ∫ – حا س . د س =  حتا س   وهكذا ...

التكامل غير المحدود :

    مشتقة الدوال د(س) = س³ + 5    ،     د(س) = س³ + 15    ،    د(س) = س³ – 12 لها ناتج واحد هو 3 س² لأن مشتقة الثابت = 0 فالمشتقة الأولى لأي دالة هي دالة معينة دوماً بصرف النظر عن كون الدالة بسيطة أم مركبة وهذا ليس صحيحاً في التكامل فالدالة 2س يكون تكاملها س² + 2   أو    س² – 12 أو ... وبصورة عامة  س² + ث حيث ث ثابت لا يتوقف على س ويعرف بثابت التكامل ولذا يسمى ∫ ع . د س بالتكامل غير المحدود لأن ناتج  ∫ ع . د س يشمل كل الدوال التي لها نفس المشتقة الأولى ولكن تختلف عن بعضها البعض في قيمة المقدار الثابت ث(الاختياري).

وللحصول على تكامل دالة ع نبحث عن دالة تكون مشتقتها الأولى ع وهو ما يعني معرفتنا بالمشتقة الأولى لها وهو ما يعرف بالدالة المقابلة للدالة ع بمعنى أكثر وضوحاً

    ق(س) دالة مقابلة للدالة د(س) في [أ ، ب] إذا كانت ق¯(س) = د(س) "س ' [أ ، ب] ، وأنَّ : ق(س) + ث هي مجموعة الدوال المقابلة للدالة د(س) ، حيث ث ثابت التكامل ، أي  ∫ د(س) د س = ق(س) + ث وهو التكامل غير المحدد للدالة د(س) .

    من أجل ذلك يجب التعرف على الدوال الأساسية وهو ما يعرف بالتكاملات القياسية البسيطة نوردها هنا في الجدول الآتي :

جدول مشتقات الدوال الأساسية والتكاملات المناظرة لها
ص =  سن	ص¯=  ن سن – 1
ص = حا س	ص¯=  حتا س	ò حتا س . د س = حا س + ث
ص = حتا س	ص¯= – حا س	ò حا س . د س = – حتا س + ث
ص = طا س	ص¯=  قا2س	ò قا2س . د س = طا س + ث
ص = طتا س	ص¯= – قتا2س	ò قتا2س . د س = – طتا س + ث
ص = قا س	ص¯=  قا س طا س	ò قا س طا س . د س = قا س + ث
ص = قتا س	ص¯= – قتا س طتا س	ò قتا س طتا س . د س = – قتا س + ث
ص = حا–1س
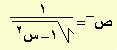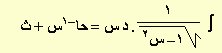ص = حتا–1س
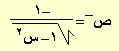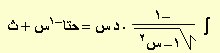ص = طا–1س
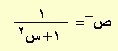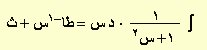ص = طتا–1س
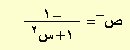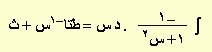ص = قا–1س
ص = قتا–1س
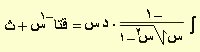ص =  هـس	ص¯= هـس	ò هـس . د س = هـس +  ث

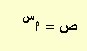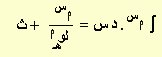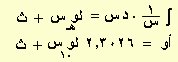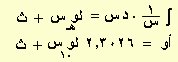    سنختار من الجدول :

ملاحظـة وأمثلة :

    هذا القانون صحيح لجميع قيم ن عدا ن = –1 حيث يكون ناتج التكامل قيمة غير    معرفة لأن المقام سيكون صفر ولكن س^–1 تكاملها لو_هـس + ث كما ورد في الجدول أعلاه ويجب هنا القول بأن تكامل د س هو س + ث أي

     ∫ د س =  ∫ س⁰ . د س =  س^{0 + 1}÷ (0 + 1) + ث = س + ث

مثال :

    ∫ 2س . د س = 2 س² ÷ 2 + ث = س² + ث

مثال آخر :

    ∫ حتا س . د س = حا س + ث

مثال ثالث :

    ∫ 4 س³ . د س = 4 س⁴ ÷ 4 + ث = س⁴ + ث

التكاملات غير القياسية :ـ

هي التي لا وجود لها في الجدول السابق أو بعيدة عنها ولا بد من عرض ثلاث قواعد تساعدنا على إيجاد تلك التكاملات غير القياسية وليس كلها فالقاعدة الأولى لمجموع عدة دوال حيث يكون :

    ∫ ( ع ±  ق ±  ف ) د س =  ∫ ع د س ±  ∫  ق د س ±  ∫  ف د س

والقاعدة الثانية بوجود ثابت مع متغير أي :

    ∫ ث ع د  س = ث ∫ ع د س  حيث ث ثابت

فمثلاً :  ∫ (4 س³ + 2 س – 5). د س =  4∫ س³ د س + 2 ∫ س د س – ∫ 5  د س

       ∫ (4 س³ + 2 س – 5). د س =  س⁴ +  س² – 5 س + ث

والقاعدة الثالثة تكامل دالة مضروبة في مشتقتها فالناتج الدالة مرفوعة لأسها +1 ومقسومة على الأس الجديد

                                             ق[د(س])^ن+1

    ∫ ق[د(س)]^ن د^/(س) د س =  ــــــــــــــــــــــــ  + ث

                                               ن + 1

مع التنبيه بالنسبة للدوال المثلثية في الجدول يقسم على الثابت حال وجوده مع المتغير مثال ذلك : ∫ حتا2س . د س = ½ حا2س + ث   

لاحظ : في تكامل 4 س³ أضفنا 1 للأس(3 + 1 = 4) وقسمنا على 4 عكس التفاضل ضربنا في الأس(4) وأنقصنا منه 1 (4 – 1 = 3) هو ما دفعنا للقول بأن التكامل عملية عكسية للتفاضل.

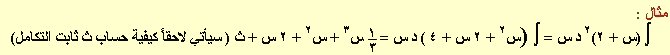
 مثال :

     ∫ (2 حا س + 3 قاس طاس – قا²س) د س = – 2 حتاس + 3 قاس – طاس + ث ( أشتق الجواب ، ماذا تلاحظ ؟ )

    يجب أن نتقن التكاملات الموجودة في الجدول السابق مع القاعدتين السابقتين ولنتعرف الآن على دوال غير موجودة في الجدول فيكون الحل لها أما بوجود قاعدة لها أو معالجتها للوصول لما ورد في الجدول ولنعطي مثال لذلك حتا²س غير موجودة في الجدول فنقول حتا2س = 2حتا²س – 1 ومن هنا

                        1                       

 نحسب حتا²س = ـــ(حتا2س + 1) فيكون :

                       2

                                1                              1                                1    1                               1   1 

   ∫ حتا²س  د س = ∫ ـــ(حتا2س + 1) د س = ـــ∫ (حتا2س + 1) د س = ـــ [ ــــ حا2س + س + ث ] = ـــ [ ـــ حا2س + س] + ث

                               2                              2                                 2    2                               2   2

والحال نفسه مع الدوال المثلثية المشابهة كمربعات للدوال المثلثية الستة ذكرنا إحداها وهذه الثلاثة الأخرى :

                  1

     حا²س = ــــ (1 – حتا2س)  ،   طا²س = قا²س – 1  ،   طتا²س = قتا²س – 1

                  2

وماذا يكون الحال مع الأسس الأخرى مثل حا³س ، حا⁴س ، ... وغيرها فالأمر يعود لإعادتها لما سبق مع إجراء جبري وسنقدم مثالين

الأول :

                                                                                                                                                             1

∫ حا³س د س =   ∫ حا²س حا س د س = ∫ (1 – حتا²س) حا س د س = ∫ (حا س – حتا²س حا س) د س = – حتا س + ـــــ حتا³س + ث

                                                                                                                                                             3

ويمكن إجراء عمل جبري للجواب السابق كما في المثال التالي حتا³(4س)

الثاني :

∫ حا⁴س د س =   ∫(حا²س)² د س

                            1

                   = ∫ [ ـــ(1 – حتا2س)]² د س

                           2

                         1

                   = ∫ ـــ[1 –2حتا2س + حتا²(2س) ] د س 

                        4

                         1                        1 

                   = ∫ ـــ[1 – 2حتا2س + ـــ (حتا4س + 1)] د س  

                        4                        2

                         1                        1               1              1                               

                   = ∫ ـــ(1 – 2حتا2س + ـــ حتا4س + ـــ) د س      ـــ مشترك

                        4                        2               2              2 

                         1

                   = ∫ ـــ( 2 –4 حتا2س + حتا4س + 1 ) د س 

                        8

                         1

                   = ∫ ـــ( 3 –4 حتا2س + حتا4س ) +  ث

                        8

                       1                   1              1

                   =  ـــ( 3 س –4 × ـــ حا2س + ـــ حا4س ) +  ث    يمكن التوقف هنا كحل للمسألة بعد التبسيط

                       8                   2              4

                       1                  1                           1

                   = ــــ(3 س –4 × ــــ × 2حاس حتاس +  ـــ × 2حا2س حتا2س ) +  ث

                      8                   2                           4

                       1                                   1

                   = ــــ[ 3 س –4 حاس حتاس + ــــ × 2 × 2حاس حتاس(1 – 2حا²س )] +  ث

                       8                                   4

                       1

                   = ــــ( 3 س –4 حاس حتاس + حاس حتاس – 2حا³س حتاس ) +  ث

                       8

                       1

                   = ــــ( 3 س –3 حاس حتاس – 2حا³س حتاس ) +  ث

                       8

                                                                                                                                                                           1 

                                                                                                                                                                           _{ـــ ن} 

وهذا يقودنا للأس الفردي (ن فردية) نضع حا^ن(س) = حا^ن–1(س) حاس ، وفي حالة الأس زوجي (ن زوجية) نضع حا^ن(س) = (حا²س)²

ملاحظة : سنورد قوانين لهذه الحالات لاحقاً ولكن غير مقبولة للحل في المرحلة الثانوية