طريقة المتوسطات النصفية: Semi Average method
طريقة المتوسطات النصفية بتقسيم السلسلة الزمنية لنصفين (زمنياً) واستبعاد السنة الوسطية (الواقعة في منتصف السلسلة الزمنية) حال عدد السنوات فردي أو سنة من البداية أو سنة من النهاية، وحساب الوسطين الحسابين لكل نصف عند منتصف فترة النصف فنحصل على نقطتين (الوسط الحسابي ، السنة الوسطى) يتم التوصيل بين النقطتين بخط مستقيم ليمثل خط الاتجاه العام وفي حالة السنوات الزوجية تكون النقطة (الوسط الحسابي ، منتصف السنتين في الوسط) كما هو مبين في المثالين الآتيين:
مثال:
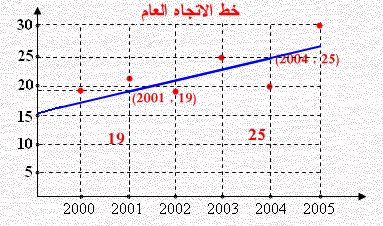
حدد خط الاتجاه العام بطريقة المتوسطات النصفية للجدول الآتي الذي يمثل القيمة بالروبية البحرينية كمية الماء المستهلكة بالمتر المكعب لأسرة للفترة 2000–2006م.
| 2006 | 2005 | 2004 | 2003 | 2002 | 2001 | 2000 | السنة |
| 30 | 20 | 25 | 19 | 18 | 22 | 17 | الاستهلاك بالدينار |
الحل:
نقسم السلسلة الزمنية إلى نصفين (تم حذف السنة الوسطى 2003) كما يلي: ( يمكن حذف سنة 2000 أو 2006 )
| 2006 | 2005 | 2004 | 2002 | 2001 | 2000 | السنة |
| 30 | 20 | 25 | 18 | 22 | 17 | الاستهلاك بالدينار |
نحسب المتوسط لكل قسم: من 2000 إلى 2002 : المتوسط = (17 + 22 + 18) ÷ 3 = 57 ÷ 3 = 19 عند منتصف الفترة (النصف من السلسلة) عند 2001
من 2003 إلى 2005 : المتوسط = (25 + 20 + 30) ÷ 3 = 75 ÷ 3 = 25 عند منتصف الفترة (النصف من السلسلة) عند 2004
نقوم برسم بياني لخط الاتجاه العام كما مبين بالشكل:

لمعرفة قيمة الاتجاه العام لسنة بأن نحسب الزيادة السنوية للاتجاه:
قيمة الاتجاه العام لسنة = متوسط النصف الواقعة فيه السنة + [(مجموع الزيادة بين المتوسطين) ÷ عدد السنين بين المتوسطين] × موقع السنة المطلوبة
قيمة الاتجاه العام لسنة 2002 = 19 + [ ( 25 – 19 ) ÷ 3 ] × 3
= 19 + 6
= 25
مثال آخر:
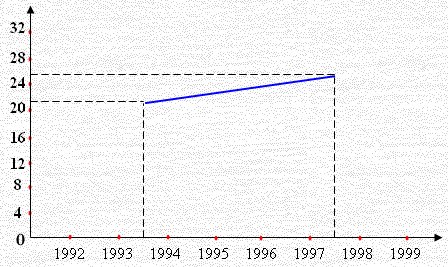
حدد خط الاتجاه العام بطريقة المتوسطات النصفية للجدول الآتي الذي يمثل أجور العاملين بآلاف بالدولار في أحدى المؤسسات للفترة 1992– 1999م.
| 1999 | 1998 | 1997 | 1996 | 1995 | 1994 | 1993 | 1992 | السنة |
| 20 | 24 | 28 | 30 | 20 | 25 | 18 | 22 | الأجور |
الحل:
نقسم السلسلة الزمنية إلى نصفين كما يلي:
| 1999 | 1998 | 1997 | 1996 | 1995 | 1994 | 1993 | 1992 |
السنة |
| 20 | 24 | 28 | 30 | 20 | 25 | 18 | 22 |
الأجور |
نحسب المتوسط لكل قسم:
1992 ــ 1995: المتوسط = (22 + 18 + 25 + 20) ÷ 4 = 85 ÷ 4 = 21.25 مقابل منتصف الفترة (النصف من السلسلة) بين 1993 ، 1994
1996 ــ 1999: المتوسط = (30 + 28 + 24 + 20) ÷ 4 = 102 ÷ 4 = 25.5 مقابل منتصف الفترة (النصف من السلسلة) بين 1996 ، 1997
نحدد النقطتين ونصل بينهم كما هو مبين في الشكل الآتي بالخط الأزرق الذي يمثل خط الاتجاه العام:
لإيجاد معادلة الانحدار T = a + βX واضح أن β هو ميل خط الاتجاه العام (الانحدار) والصيغة التي يمكن حساب β منها هي الفرق بين الوسطين بالنسبة للفرق بين زمنيهم أي
β = ( `X2 – `X1 ) / ( t2 – t1)
أما a فهي تساوي الوسط الحسابي لكل نصف (من السلسلة الزمنية) أي a2 = 25.5 ، a1 = 21.25 فتتكون معادلتين هما: Y2 = a2 + βX , Y1 = a1 + βX
بتطبيق الصيغة الخاصة بـ β
β = ( `X2 – `X1 ) / ( t2 – t1)
= ( 25.5 – 21.25) / (1998 – 1994)
= 4.25 / 4
= 1.06
وبتطبيق الصيغة الأخرى (المعادلتين) حيث أن: a2 = 25.5 ، a1 = 21.25
Y1 = 21.25 + 1.06 X
Y2 = 25.50 + 1.06 X
يمكن استخدام هاتين المعادلتين للتنبؤ المستقبلي كحساب القيمة الاتجاهية للظاهرة في سنة 2006 مثلاً باعتبار 1992 سنة أساس فسنة 2006 تكون عندها X = 14 أي:
Y = 21.25 + 1.06 × 14 = 21.25 + 14.84 = 36.09