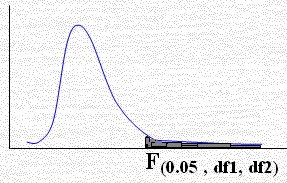
توزيع f

    ليكن لدينا المتغيران العشوائيان المستقلان X₁ , X₂ وكل منهم يتبع توزيع معتدل وأخذنا عينة عشوائية حجمها n₁ من المجتمع X₁ ، عينة عشوائية حجمها n₂ من المجتمع X₂ ثم حصلنا على تقدير غير متميز لباين المجتمع الأول σ₁² هو S₁² وكذلك للمجتمع الثاني ل σ₂² هو S₂²  فالنسبة بين التباينين تتبع توزيع f بدرجات حرية لكل من البسط والمقام V₁ = n1 – 1 (للبسط) , V₂ = n₂ – 1 (للمقام) وهذا التوزيع يستخدم لاختبار تساوي مجتمعين وإحصائية الاختبار F هي: F = S₁² ÷ S₂² والتوزيع هذا يختلف باختلاف درجات الحرية سواء للبسط أو المقام أو كلاهما فمثلاً  نرمز للتوزيع f  بدرجة حرية للبسط 4 ، ودرجة حرية للمقام 8 عند مستوى معنوية 0.05 بالصورة:

F_{( 0.05 ,  4 , 8 )}

والجدول الخاص به يعرف بجدول توزيع F ونجده هنا وهو يختلف عن توزيع t , χ² والتوزيع صفه الأول يمثل درجات الحرية للبسط والعمود الأول لدرجات حرية المقام ويبين كل جزء منع مستوى معنوية ( α ) للقيم 0.01 ، 0.025 ، 0.05 ، 0.10 ويرمز للقيمة المستخرجة من الجدول بالشكل الآتي (المساحة على يمينها = α):

F_{( α , V1 , V2 )}

يجب التأكيد على أنه إذا كانت النسبة  أقل من الواحد الصحيح (معنوياً) فهذا يدل على تساوي تباين المجتمعين وإلا يوجد دلالة على اختلاف حقيقي بين تبايني المجتمعين أما قبول أو رفض فرض العدم ينتج من مقارنة قيمة F المحتسبة مع قيمة F الجدولية.